题目内容
8.设a,b都是奇数,且关于x的方程x2+(4a-3b)x+4a2+b2+9=0的两个根都是质数,求这个方程的两个根.分析 利用奇数与偶数得性质可判断4a2+b2+9为偶数,再利用根与系数的关系得到两质数的积为4a2+b2+9,所以可判断方程必有一个根为2,再把x=2代入方程得变形得到变形得4(a+1)2+(b-3)2=0,利用非负数的性质可解得a=-1,b=3,所以方程化为x2-13x+22=0,然后利用因式分解法解方程即可.
解答 解:∵a,b都是奇数,
∴4a2+b2+9为偶数,
∵方程的两根之积为4a2+b2+9,
而方程的两个根都是质数,
∴方程必有一个根为2,
把x=2代入方程得4+2(4a-3b)+4a2+b2+9=0,
变形得4(a+1)2+(b-3)2=0,
∴a+1=0,b-3=0,解得a=-1,b=3,
∴方程化为x2-13x+22=0,解得x1=2,x2=11,
即这个方程的两个根为2和11.
点评 本题考查了一元二次方程的解:能使一元二次方程左右两边相等的未知数的值是一元二次方程的解.也考查了奇数、质数和根与系数的关系.

练习册系列答案
相关题目
16.在?ABCD中,E是AD边中点,若平行四边形的面积为acm2,F是BE与AC的交点,则△CEF的面积等于( )
| A. | $\frac{1}{3}$acm2 | B. | $\frac{1}{4}$acm2 | C. | $\frac{1}{6}$acm2 | D. | $\frac{1}{8}$acm2 |
17.若平行四边形的对角线和一边垂直,且邻边之比为1:2,则平行四边形的内角中较小的角的大小为( )
| A. | 45° | B. | 60° | C. | 30° | D. | 75° |
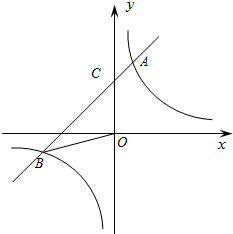 如图,已知反比例函数y=$\frac{k}{x}$的图象与一次函数y=mx+b的图象相交于两点A(1,3),B(n,-1).
如图,已知反比例函数y=$\frac{k}{x}$的图象与一次函数y=mx+b的图象相交于两点A(1,3),B(n,-1). 如图,在四边形ABCD中,E、F、G、H分别是各边的中点,对角线AC⊥BD于点O.求证:四边形EFGH是矩形.
如图,在四边形ABCD中,E、F、G、H分别是各边的中点,对角线AC⊥BD于点O.求证:四边形EFGH是矩形.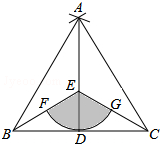 如图,点D是线段BC的中点,分别以点B,C为圆心,BC长为半径画弧,两弧相交于点A,连接AB,AC,AD,点E为AD上一点,连接BE,CE.
如图,点D是线段BC的中点,分别以点B,C为圆心,BC长为半径画弧,两弧相交于点A,连接AB,AC,AD,点E为AD上一点,连接BE,CE.