题目内容
7.在△ABC中,∠C=90°,a:b=3:4,c=15,则△ABC的面积是54.分析 设a=3k,b=4k,由勾股定理得出(3k)2+(4k)2=152,求出k,进而求出a、b的值,根据面积公式求出即可.
解答 解:设a=3k,b=4k,
由勾股定理得:(3k)2+(4k)2=152,
解得:k=3,
所以a=9,b=12,
即△ABC的面积为$\frac{1}{2}$×9×12=54,
故答案为:54.
点评 本题考查了勾股定理的应用,能根据勾股定理得出方程是解此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
16.在?ABCD中,E是AD边中点,若平行四边形的面积为acm2,F是BE与AC的交点,则△CEF的面积等于( )
| A. | $\frac{1}{3}$acm2 | B. | $\frac{1}{4}$acm2 | C. | $\frac{1}{6}$acm2 | D. | $\frac{1}{8}$acm2 |
17.若平行四边形的对角线和一边垂直,且邻边之比为1:2,则平行四边形的内角中较小的角的大小为( )
| A. | 45° | B. | 60° | C. | 30° | D. | 75° |
 如图,某同学站在旗杆正对的教学楼上点C处观测到旗杆顶端A的仰角为30°,旗杆底端B的俯角为45°,已知旗杆距离教学楼12米,求旗杆AB的高度.
如图,某同学站在旗杆正对的教学楼上点C处观测到旗杆顶端A的仰角为30°,旗杆底端B的俯角为45°,已知旗杆距离教学楼12米,求旗杆AB的高度.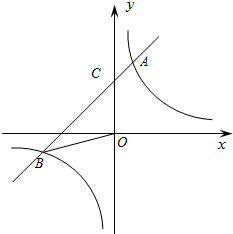 如图,已知反比例函数y=$\frac{k}{x}$的图象与一次函数y=mx+b的图象相交于两点A(1,3),B(n,-1).
如图,已知反比例函数y=$\frac{k}{x}$的图象与一次函数y=mx+b的图象相交于两点A(1,3),B(n,-1). 如图,直线l∥x轴,分别与函数$y=\frac{2}{x}$(x>0)和$y=\frac{k}{x}$(x<0)的图象相交于点A、B,交y轴于点C,若AC=2BC,则k=-1.
如图,直线l∥x轴,分别与函数$y=\frac{2}{x}$(x>0)和$y=\frac{k}{x}$(x<0)的图象相交于点A、B,交y轴于点C,若AC=2BC,则k=-1. 如图.∠1+∠2+∠3+∠4+∠5+∠6的值为720°(分割成三角形).
如图.∠1+∠2+∠3+∠4+∠5+∠6的值为720°(分割成三角形). 已知:如图,∠ABC=∠C,BD是∠ABC的平分线.求证:∠BDC=180°-$\frac{3}{2}$∠C.
已知:如图,∠ABC=∠C,BD是∠ABC的平分线.求证:∠BDC=180°-$\frac{3}{2}$∠C. 如图,在四边形ABCD中,E、F、G、H分别是各边的中点,对角线AC⊥BD于点O.求证:四边形EFGH是矩形.
如图,在四边形ABCD中,E、F、G、H分别是各边的中点,对角线AC⊥BD于点O.求证:四边形EFGH是矩形.