��Ŀ����
9����ͼ����Rt��ABC�У���C=90�㣬AC=6cm��BC=8cm��D��E�ֱ���AC��AB���е㣬����DE����P�ӵ�D��������DE���������˶����ٶ�Ϊ1cm/s��ͬʱ����Q�ӵ�B��������BA���������˶����ٶ�Ϊ2cm/s������Pֹͣ�˶�ʱ����QҲֹͣ�˶�������PQ�����˶�ʱ��Ϊt��s����0��t��4���������������Ϣ�������������⣺��1����tΪ��ֵʱ��PQ��AB��
��2������Q��BE֮���˶�ʱ���������PQBCD�����Ϊy��cm2������y��t֮��ĺ�������ʽ��
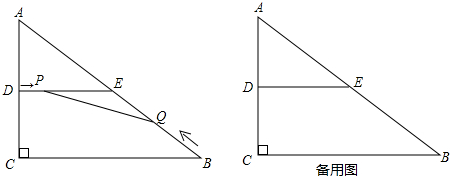
���� ��1����ͼ����ʾ����PQ��ABʱ����PQE��ֱ�������Σ���������Ҫ���ǽ���PQE�����߳�PE��QE��PQ��ʱ��t��ʾ������Ҫ�������������Σ���PQE�ס�ACB�������߶ι�ϵ�������Ǻ�������
��2�����ʹؼ������õ�ʽ�������PQBCD�����=�ı���DCBE�����-��PQE�����������ͼ����ʾ��Ϊ���PQE���������Ҫ���QE���ϵĸߣ���˹�P����QE���ϵĸߣ��������ƹ�ϵ����PME�ס�ABC������ߵı���ʽ���Ӷ���������
���  �⣺��1����ͼ�٣���Rt��ABC�У�
�⣺��1����ͼ�٣���Rt��ABC�У�
AC=6��BC=8
��AB=$\sqrt{{6}^{2}+{8}^{2}}$=10��
��D��E�ֱ���AC��AB���е㣮
AD=DC=3��AE=EB=5��DE��BC��
DE=$\frac{1}{2}$BC=4
��PQ��AB��
���PQB=��C=90��
�֡�DE��BC��
���AED=��B��
���PQE�ס�ACB��
$\frac{PE}{AB}$=$\frac{QE}{BC}$��������ã�PE=4-t��QE=2t-5��
��$\frac{4-t}{10}=\frac{2t-5}{8}$��
���t=$\frac{41}{14}$��
��2����ͼ�ڣ�����P��PM��AB��M��
�ɡ�PME�ס�ACB����$\frac{PM}{AC}$=$\frac{PE}{AB}$��
��$\frac{PM}{6}$=$\frac{4-t}{10}$����PM=$\frac{3}{5}$��4-t����
S��PQE=$\frac{1}{2}$EQ•PM=$\frac{1}{2}$��5-2t��•$\frac{3}{5}$��4-t��=$\frac{3}{5}$t2-$\frac{39}{10}$t+6��
S����DCBE=$\frac{1}{2}$����4+8����3=18��
��y=18-��$\frac{3}{5}$t2-$\frac{39}{10}$t+6��=-$\frac{3}{5}$t2+$\frac{39}{10}$t+12��
���� �����Ƕ������ۺ��⣬����ؼ������ն����˶������е�ͼ����״��ͼ������ı�ʾ�������������֪ʶ���漰�����ɶ��������������ε��ж������ʡ���������λ�߶������ⷽ�̣�����һԪһ�η��̺�һԪ���η��̣��ȣ���һ�����Ѷȣ�ע��������ʱ��t�ķ��������ն���ת��ΪһԪһ�η��̻�һԪ���η�����⣮

 ��У����ϵ�д�
��У����ϵ�д�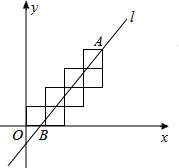 �߸��߳�Ϊ1�������ΰ���ͼ��ʾ�ķ�ʽ������ƽ��ֱ������ϵxOy�У�ֱ��l������A��4��4���ҽ����߸������ε�����ֳ���ȵ������֣���ֱ��l��x��Ľ���B�ĺ�����Ϊ��������
�߸��߳�Ϊ1�������ΰ���ͼ��ʾ�ķ�ʽ������ƽ��ֱ������ϵxOy�У�ֱ��l������A��4��4���ҽ����߸������ε�����ֳ���ȵ������֣���ֱ��l��x��Ľ���B�ĺ�����Ϊ��������| A�� | $\frac{2}{3}$ | B�� | $\frac{3}{4}$ | C�� | $\frac{4}{5}$ | D�� | $\frac{7}{9}$ |
 ��ͼ�⣨��ͼ���߲��ޣ�������ͼ�ۼ���д�����ۣ�
��ͼ�⣨��ͼ���߲��ޣ�������ͼ�ۼ���д�����ۣ�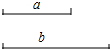 ��1���Ȼ�������ֵ����3a2-ab+7��-��5ab-4a2+7��������a=2��b=$\frac{1}{3}$��
��1���Ȼ�������ֵ����3a2-ab+7��-��5ab-4a2+7��������a=2��b=$\frac{1}{3}$��