题目内容
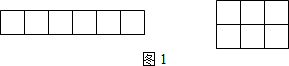
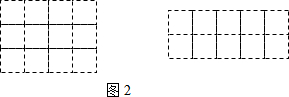
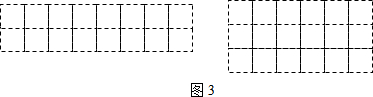
14.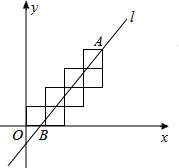 七个边长为1的正方形按如图所示的方式放置在平面直角坐标系xOy中,直线l经过点A(4,4)且将这七个正方形的面积分成相等的两部分,则直线l与x轴的交点B的横坐标为( )
七个边长为1的正方形按如图所示的方式放置在平面直角坐标系xOy中,直线l经过点A(4,4)且将这七个正方形的面积分成相等的两部分,则直线l与x轴的交点B的横坐标为( )| A. | $\frac{2}{3}$ | B. | $\frac{3}{4}$ | C. | $\frac{4}{5}$ | D. | $\frac{7}{9}$ |
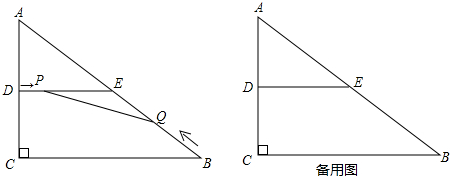
分析 如图,过点A作AD⊥x轴于点D,由直线l将七个正方形面积分为相等的两部分确定出三角形ABD面积,进而求出BD的长,得出OB的长,即为B横坐标.
解答 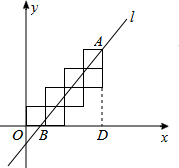 解:如图,过点A作AD⊥x轴于点D,
解:如图,过点A作AD⊥x轴于点D,
由题意,可知△ABD的面积为$\frac{7}{2}$+3=$\frac{13}{2}$,
∴$\frac{1}{2}$AD•BD=$\frac{13}{2}$,即BD=$\frac{13}{AD}$=$\frac{13}{4}$,
∴OB=4-$\frac{13}{4}$=$\frac{3}{4}$,
则点B的横坐标为$\frac{3}{4}$.
故选B.
点评 此题考查了坐标与图形性质,以及三角形面积,根据题意求出△ABD面积是解本题的关键.

练习册系列答案
相关题目
5.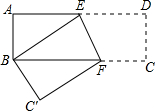 将矩形纸片ABCD按下图方式折叠,使点D与点B重合,折痕为EF,若S△ABE:S△BFE=4:5,则tan∠BFE=( )
将矩形纸片ABCD按下图方式折叠,使点D与点B重合,折痕为EF,若S△ABE:S△BFE=4:5,则tan∠BFE=( )
 将矩形纸片ABCD按下图方式折叠,使点D与点B重合,折痕为EF,若S△ABE:S△BFE=4:5,则tan∠BFE=( )
将矩形纸片ABCD按下图方式折叠,使点D与点B重合,折痕为EF,若S△ABE:S△BFE=4:5,则tan∠BFE=( )| A. | $\frac{1}{3}$ | B. | $\sqrt{3}$ | C. | 3 | D. | $3\sqrt{3}$ |
2.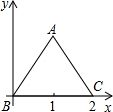 如图,边长为2的等边△ABC以点B为旋转中心,逆时针旋转60°时,点A的对应点的坐标( )
如图,边长为2的等边△ABC以点B为旋转中心,逆时针旋转60°时,点A的对应点的坐标( )
 如图,边长为2的等边△ABC以点B为旋转中心,逆时针旋转60°时,点A的对应点的坐标( )
如图,边长为2的等边△ABC以点B为旋转中心,逆时针旋转60°时,点A的对应点的坐标( )| A. | (1,$\sqrt{3}$) | B. | (1,-$\sqrt{3}$) | C. | (-1,$\sqrt{3}$) | D. | (-1,-$\sqrt{3}$) |
6.某公司有A型产品40件,B型产品60件,分配给下属甲、乙两个商店销售,其中70件给甲店,30件给乙店,且都能卖完.设分配给甲店A型产品x件.两商店销售这两种产品每件的利润(元)如下表:
(1)分配给乙店B型产品x-10件(用含x的代数式表示).
(2)设这家公司卖出这100件产品的总利润为W(元),求W关于x的函数关系式,并直接写出x的取值范围.
(3)若公司要求总利润不低于17560元,有几种不同分配方案?哪种方案总利润最大?请求出最大利润.
| A型利润 | B型利润 | |
| 甲店 | 200 | 170 |
| 乙店 | 160 | 150 |
(2)设这家公司卖出这100件产品的总利润为W(元),求W关于x的函数关系式,并直接写出x的取值范围.
(3)若公司要求总利润不低于17560元,有几种不同分配方案?哪种方案总利润最大?请求出最大利润.
 如图,△ABC中,∠ACB=90°,沿CD边折叠△CBD,使点B恰好落在AC边上的点E处,若∠A=22°,则∠BDC等于67°.
如图,△ABC中,∠ACB=90°,沿CD边折叠△CBD,使点B恰好落在AC边上的点E处,若∠A=22°,则∠BDC等于67°.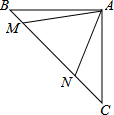 如图,等腰直角三角形ABC中,∠BAC=90°,AB=AC,点M,N在边BC上,且∠MAN=45°.若BM=1,CN=3,则MN的长为$\sqrt{10}$.
如图,等腰直角三角形ABC中,∠BAC=90°,AB=AC,点M,N在边BC上,且∠MAN=45°.若BM=1,CN=3,则MN的长为$\sqrt{10}$.