题目内容
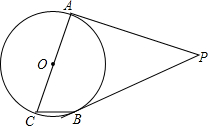如图，PA、PB是⊙O的切线，点A，B为切点，AC是⊙O的直径，∠ACB=65°，求∠P的度数．考点：切线的性质
专题：
分析：如图，作辅助线，运用弦切角定理证明∠PAB=∠PBA=∠ACB=65°，结合三角形的内角和定理问题即可解决．
解答：
解：如图，连接AB；
∵PA、PB是⊙O的切线，
∴∠PAB=∠PBA=∠ACB=65°，
∴∠P=180°-2×65°=50°，
即∠P的度数为50°．
解：如图，连接AB；∵PA、PB是⊙O的切线，
∴∠PAB=∠PBA=∠ACB=65°，
∴∠P=180°-2×65°=50°，
即∠P的度数为50°．
点评：该命题主要考查了切线长定理、弦切角定理及其应用问题；解题的关键是灵活运用弦切角定理来分析、判断、计算或解答．
练习册系列答案
相关题目
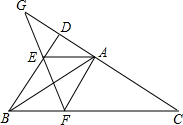在△ABC中，以边AB为轴翻折∠ABC，使翻折后BC的对应边交CA的延长线于点D．分别过A作AE∥BC交BD于E，作AF∥BD交BC于F，延长CD、EF交于G．若BC=2BD，BE=1，求DE的长
如图，△ABC中，D、E分别是边BC、AB的中点，AD、CE相交于G．求证：
如图，AB是⊙O的直径，点C在⊙O上，AB=6，∠B=30°，则BC的长为（ ）| A、12 | ||
B、3
| ||
C、2
| ||
D、12
|