题目内容
在△ABC中,∠A=135°,AB=20,AC=30,则△ABC的面积是 .
考点:解直角三角形
专题:
分析:过点B作BE⊥AC,根据勾股定理可求得BE,再根据三角形的面积公式求出答案.
解答: 解:过点B作BE⊥AC于E,
解:过点B作BE⊥AC于E,
∵∠BAC=135°,
∴∠BAE=180°-∠A=180°-135°=45°,
∴∠ABE=90°-∠BAE=90°-45°=45°,
在Rt△BAE中,BE2+AE2=AB2,
∵AB=20,
∴BE=
AB=10
,
∵AC=30,
∴S△ABC=
AC•BE=
×30×10
=150
.
故答案为150
.
 解:过点B作BE⊥AC于E,
解:过点B作BE⊥AC于E,∵∠BAC=135°,
∴∠BAE=180°-∠A=180°-135°=45°,
∴∠ABE=90°-∠BAE=90°-45°=45°,
在Rt△BAE中,BE2+AE2=AB2,
∵AB=20,
∴BE=
| ||
| 2 |
| 2 |
∵AC=30,
∴S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| 2 |
故答案为150
| 2 |
点评:本题考查了解直角三角形,勾股定理以及三角形的面积公式,是基础知识比较简单.

练习册系列答案
相关题目
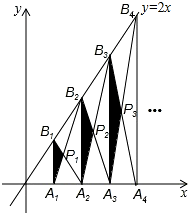 如图,已知A1、A2、A3、…、An、An+1是x轴上的点,且OA1=A1A2=A2A3=…=AnAn+1=1,分别过点A1、A2、A3、…、An、An+1作x轴的垂线交直线y=2x于点B1、B2、B3、…、Bn、Bn+1,连接A1B2、B1A2、B2A3、…、AnBn+1、BnAn+1,依次相交于点P1、P2、P3、…、Pn.△A1B1P1、△A2B2P2、△AnBnPn的面积依次记为S1、S2、S3、…、Sn,则Sn为( )
如图,已知A1、A2、A3、…、An、An+1是x轴上的点,且OA1=A1A2=A2A3=…=AnAn+1=1,分别过点A1、A2、A3、…、An、An+1作x轴的垂线交直线y=2x于点B1、B2、B3、…、Bn、Bn+1,连接A1B2、B1A2、B2A3、…、AnBn+1、BnAn+1,依次相交于点P1、P2、P3、…、Pn.△A1B1P1、△A2B2P2、△AnBnPn的面积依次记为S1、S2、S3、…、Sn,则Sn为( )A、
| ||
B、
| ||
C、
| ||
D、
|
绝对值等于本身的数是( )
| A、正数 | B、正数或零 |
| C、零 | D、负数或零 |
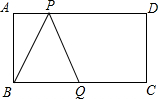 如图:长方形ABCD中,AD=10,AB=4,点Q是BC的中点,点P在AD边上运动,当△BPQ是等腰三角形时,AP的长为
如图:长方形ABCD中,AD=10,AB=4,点Q是BC的中点,点P在AD边上运动,当△BPQ是等腰三角形时,AP的长为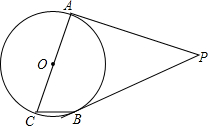 如图,PA、PB是⊙O的切线,点A,B为切点,AC是⊙O的直径,∠ACB=65°,求∠P的度数.
如图,PA、PB是⊙O的切线,点A,B为切点,AC是⊙O的直径,∠ACB=65°,求∠P的度数.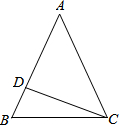 在等腰△ABC中,AB=AC,CD⊥AB于D.
在等腰△ABC中,AB=AC,CD⊥AB于D.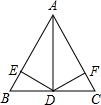 如图,在△ABC中,AB=AC,AD是△ABC的角平分线,DE⊥AB于E,DF⊥AC于F,则下列四个结论中:①DE=DF; ②AD上任意一点到AB、AC的距离相等; ③∠BDE=∠CDF;④BD=CD,AD⊥BC.其中正确的有( )
如图,在△ABC中,AB=AC,AD是△ABC的角平分线,DE⊥AB于E,DF⊥AC于F,则下列四个结论中:①DE=DF; ②AD上任意一点到AB、AC的距离相等; ③∠BDE=∠CDF;④BD=CD,AD⊥BC.其中正确的有( )