题目内容
在△ABC中,∠C=90°,角平分线AD分对边BC为BD:DC=3:2,且BC=10cm,则点D到AB的距离是 cm.
考点:角平分线的性质
专题:
分析:根据题意画出图形,过点D作DE⊥AB于点E,由角平分线的性质可知DE=CD,根据角平分线AD分对边BC为BD:DC=3:2,且BC=10cm即可得出结论.
解答: 解:如图所示,过点D作DE⊥AB于点E,
解:如图所示,过点D作DE⊥AB于点E,
∵AD是∠BAC的平分线,∠C=90°,
∴DE=CD.
∵BD:DC=3:2,且BC=10cm,
∴CD=10×
=4(cm).
故答案为:4.
 解:如图所示,过点D作DE⊥AB于点E,
解:如图所示,过点D作DE⊥AB于点E,∵AD是∠BAC的平分线,∠C=90°,
∴DE=CD.
∵BD:DC=3:2,且BC=10cm,
∴CD=10×
| 2 |
| 5 |
故答案为:4.
点评:本题考查的是角平分线的性质,熟知角的平分线上的点到角的两边的距离相等是解答此题的关键.

练习册系列答案
相关题目
 如图,⊙O的弦AB∥CD,且AB=6,CD=8,AB与CD的距离为7,求⊙O的半径.
如图,⊙O的弦AB∥CD,且AB=6,CD=8,AB与CD的距离为7,求⊙O的半径.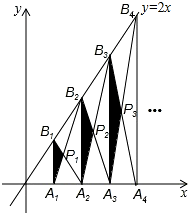 如图,已知A1、A2、A3、…、An、An+1是x轴上的点,且OA1=A1A2=A2A3=…=AnAn+1=1,分别过点A1、A2、A3、…、An、An+1作x轴的垂线交直线y=2x于点B1、B2、B3、…、Bn、Bn+1,连接A1B2、B1A2、B2A3、…、AnBn+1、BnAn+1,依次相交于点P1、P2、P3、…、Pn.△A1B1P1、△A2B2P2、△AnBnPn的面积依次记为S1、S2、S3、…、Sn,则Sn为( )
如图,已知A1、A2、A3、…、An、An+1是x轴上的点,且OA1=A1A2=A2A3=…=AnAn+1=1,分别过点A1、A2、A3、…、An、An+1作x轴的垂线交直线y=2x于点B1、B2、B3、…、Bn、Bn+1,连接A1B2、B1A2、B2A3、…、AnBn+1、BnAn+1,依次相交于点P1、P2、P3、…、Pn.△A1B1P1、△A2B2P2、△AnBnPn的面积依次记为S1、S2、S3、…、Sn,则Sn为( ) 如图,△ABC经过旋转后到△A′B′C′位置,
如图,△ABC经过旋转后到△A′B′C′位置,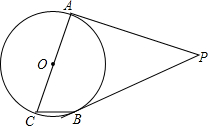 如图,PA、PB是⊙O的切线,点A,B为切点,AC是⊙O的直径,∠ACB=65°,求∠P的度数.
如图,PA、PB是⊙O的切线,点A,B为切点,AC是⊙O的直径,∠ACB=65°,求∠P的度数.