题目内容
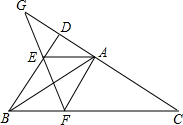 在△ABC中,以边AB为轴翻折∠ABC,使翻折后BC的对应边交CA的延长线于点D.分别过A作AE∥BC交BD于E,作AF∥BD交BC于F,延长CD、EF交于G.若BC=2BD,BE=1,求DE的长
在△ABC中,以边AB为轴翻折∠ABC,使翻折后BC的对应边交CA的延长线于点D.分别过A作AE∥BC交BD于E,作AF∥BD交BC于F,延长CD、EF交于G.若BC=2BD,BE=1,求DE的长考点:翻折变换(折叠问题)
专题:
分析:首先运用角平分线的性质证明
=
;再利用平行线分线段成比例定理证明
=
,问题即可解决.
| DB |
| BC |
| DA |
| AC |
| DE |
| BE |
| DA |
| AC |
解答: 解:如图,由题意知:
解:如图,由题意知:
AB平分∠DBC,
∴
=
;
∵AE∥BC,
∴
=
,
∴
=
=
=
,
∴DE=
BE=
,
即DE的长为
,
故答案为
.
 解:如图,由题意知:
解:如图,由题意知:AB平分∠DBC,
∴
| DB |
| BC |
| DA |
| AC |
∵AE∥BC,
∴
| DE |
| BE |
| DA |
| AC |
∴
| DE |
| BE |
| DB |
| BC |
| DB |
| 2DB |
| 1 |
| 2 |
∴DE=
| 1 |
| 2 |
| 1 |
| 2 |
即DE的长为
| 1 |
| 2 |
故答案为
| 1 |
| 2 |
点评:该命题以三角形为载体,以翻折变换为方法,以考查角平分线的性质、平行线分线段成比例定理为核心构造而成.

练习册系列答案
相关题目
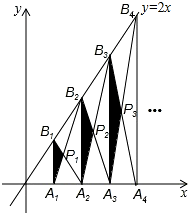 如图,已知A1、A2、A3、…、An、An+1是x轴上的点,且OA1=A1A2=A2A3=…=AnAn+1=1,分别过点A1、A2、A3、…、An、An+1作x轴的垂线交直线y=2x于点B1、B2、B3、…、Bn、Bn+1,连接A1B2、B1A2、B2A3、…、AnBn+1、BnAn+1,依次相交于点P1、P2、P3、…、Pn.△A1B1P1、△A2B2P2、△AnBnPn的面积依次记为S1、S2、S3、…、Sn,则Sn为( )
如图,已知A1、A2、A3、…、An、An+1是x轴上的点,且OA1=A1A2=A2A3=…=AnAn+1=1,分别过点A1、A2、A3、…、An、An+1作x轴的垂线交直线y=2x于点B1、B2、B3、…、Bn、Bn+1,连接A1B2、B1A2、B2A3、…、AnBn+1、BnAn+1,依次相交于点P1、P2、P3、…、Pn.△A1B1P1、△A2B2P2、△AnBnPn的面积依次记为S1、S2、S3、…、Sn,则Sn为( )A、
| ||
B、
| ||
C、
| ||
D、
|
某班学生每周课外阅读时间的统计结果如下表:则这些学生每周课外阅读的平均时间为( )
| 时间/小时 | 3 | 4 | 5 | 6 | 7 |
| 人数 | 2 | 5 | 15 | 11 | 7 |
| A、4.5小时 | B、5小时 |
| C、5.4小时 | D、5.5小时 |
 如图,△ABC经过旋转后到△A′B′C′位置,
如图,△ABC经过旋转后到△A′B′C′位置,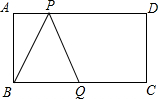 如图:长方形ABCD中,AD=10,AB=4,点Q是BC的中点,点P在AD边上运动,当△BPQ是等腰三角形时,AP的长为
如图:长方形ABCD中,AD=10,AB=4,点Q是BC的中点,点P在AD边上运动,当△BPQ是等腰三角形时,AP的长为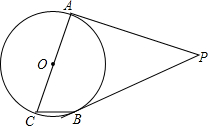 如图,PA、PB是⊙O的切线,点A,B为切点,AC是⊙O的直径,∠ACB=65°,求∠P的度数.
如图,PA、PB是⊙O的切线,点A,B为切点,AC是⊙O的直径,∠ACB=65°,求∠P的度数.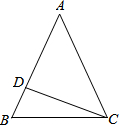 在等腰△ABC中,AB=AC,CD⊥AB于D.
在等腰△ABC中,AB=AC,CD⊥AB于D.