题目内容
19．已知（a+3）2+$\sqrt{2b-1}$=0，则一次函数y=ax+b的图象不经过的象限是（ ）| A． | 第一象限 | B． | 第二象限 | C． | 第三象限 | D． | 第四象限 |
分析 首先根据非负数的性质确定a、b的值，然后确定其不经过的象限即可．
解答 解：∵（a+3）2+$\sqrt{2b-1}$=0，
∴a+3=0，2b-1=0，
解得：a=-3＜0，b=$\frac{1}{2}$＞0，
∴一次函数y=ax+b的图象经过一、二、四象限，
故选C．
点评 本题考查了一次函数的性质．一次函数y=kx+b的图象经过的象限由k、b的值共同决定，有六种情况：
①当k＞0，b＞0，函数y=kx+b的图象经过第一、二、三象限，y的值随x的值增大而增大；
②当k＞0，b＜0，函数y=kx+b的图象经过第一、三、四象限，y的值随x的值增大而增大；
③当k＜0，b＞0时，函数y=kx+b的图象经过第一、二、四象限，y的值随x的值增大而减小；
④当k＜0，b＜0时，函数y=kx+b的图象经过第二、三、四象限，y的值随x的值增大而减小；
⑤当k＞0，b=0，函数y=kx+b的图象经过第一、三象限；
⑥当k＜0，b=0，函数y=kx+b的图象经过第二、四象限．
练习册系列答案
相关题目
9．方程组$\left\{\begin{array}{l}{2x-y=3}\\{x+3y=5}\end{array}\right.$的解是（ ）
| A． | $\left\{\begin{array}{l}{x=-1}\\{y=2}\end{array}\right.$ | B． | $\left\{\begin{array}{l}{x=1}\\{y=-1}\end{array}\right.$ | C． | $\left\{\begin{array}{l}{x=2}\\{y=1}\end{array}\right.$ | D． | $\left\{\begin{array}{l}{x=1}\\{y=2}\end{array}\right.$ |
10．
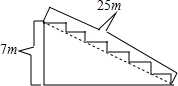如图，某公司举行周年庆典，准备在门口长25米，高7米的台阶上铺设红地毯，已知台阶的宽为3米，则共需购买（ ）m2的红地毯．
如图，某公司举行周年庆典，准备在门口长25米，高7米的台阶上铺设红地毯，已知台阶的宽为3米，则共需购买（ ）m2的红地毯．| A． | 21 | B． | 75 | C． | 93 | D． | 96 |
7．
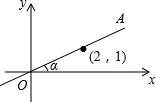如图，在平面直角坐标系中，直线OA过点（2，1），则tanα的值是（ ）
如图，在平面直角坐标系中，直线OA过点（2，1），则tanα的值是（ ）| A． | $\frac{\sqrt{5}}{5}$ | B． | $\sqrt{5}$ | C． | $\frac{1}{2}$ | D． | 2 |
如图，PA，PB分别与⊙O相切于A，B两点，∠ACB=60°．
4．已知a＜b，下列不等式中，变形正确的是（ ）
| A． | a-3＞b-3 | B． | $\frac{a}{3}＞\frac{b}{3}$ | C． | -3a＞-3b | D． | 3a-1＞3b-1 |
如图，将一个三角板的直角顶点放在直尺的一条边上，若∠1=50°，则∠2的度数为40°．
如图，直线y=kx+b与直线y=4x+2相交于点A（-1，-2），则不等式4x+2＜kx+b的解集为x＜-1．