题目内容
15.已知直线y=2x+1与直线y=-$\frac{1}{2}$x+6交于点(2,5),求这两条直线与x轴围成的三角形面积.分析 求得两条直线与x轴的交点坐标,进一步计算三角形面积即可.
解答 解:令y=0,则2x+1=0,解得x=-$\frac{1}{2}$,
∴直线y=2x+1与x轴交点坐标为(-$\frac{1}{2}$,0),
同理可得,直线y=$-\frac{1}{2}$x+6与x轴交点坐标为(12,0);
∵两直线交点为(2,5),
∴这两条直线与x轴围成的三角形面积=$\frac{1}{2}$×5×(12$+\frac{1}{2}$)=$\frac{125}{4}$.
点评 本题主要考查了两条直线相交问题,首先求得两条直线与x轴的交点坐标是解答此题的关键.

练习册系列答案
相关题目
5.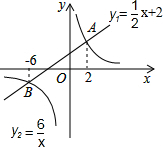 如图,直线y1=$\frac{1}{2}$x+2与双曲线y2=$\frac{6}{x}$交于A(2,m)、B(-6,n)两点,则当y1<y2时,x的取值范围是( )
如图,直线y1=$\frac{1}{2}$x+2与双曲线y2=$\frac{6}{x}$交于A(2,m)、B(-6,n)两点,则当y1<y2时,x的取值范围是( )
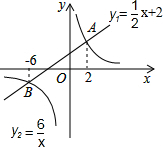 如图,直线y1=$\frac{1}{2}$x+2与双曲线y2=$\frac{6}{x}$交于A(2,m)、B(-6,n)两点,则当y1<y2时,x的取值范围是( )
如图,直线y1=$\frac{1}{2}$x+2与双曲线y2=$\frac{6}{x}$交于A(2,m)、B(-6,n)两点,则当y1<y2时,x的取值范围是( )| A. | x<-6或x>2 | B. | -6<x<0或x>2 | C. | x<-6或0<x<2 | D. | -6<x<2 |
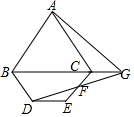 如图,等边三角形ABC中,AB=3,点D是△ABC外一点,连接BD,将线段BD绕点D顺时针旋转120°得到线段DE,连接CE,点F事CE的中点,射线DF与BC边的延长线交于点G,连接AG,若∠CBD=60°,∠ACE=90°,则线段AG的长为$\sqrt{13}$.
如图,等边三角形ABC中,AB=3,点D是△ABC外一点,连接BD,将线段BD绕点D顺时针旋转120°得到线段DE,连接CE,点F事CE的中点,射线DF与BC边的延长线交于点G,连接AG,若∠CBD=60°,∠ACE=90°,则线段AG的长为$\sqrt{13}$.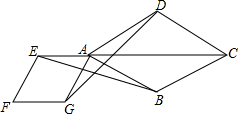 如图,点E是菱形ABCD对角线CA的延长线上任意一点,以线段AE为边作一个菱形AEFG,且∠EAG=∠BAD,连接EC,CD.
如图,点E是菱形ABCD对角线CA的延长线上任意一点,以线段AE为边作一个菱形AEFG,且∠EAG=∠BAD,连接EC,CD.