题目内容
7.要使方程组$\left\{\begin{array}{l}{2x+ay=16}\\{x-2y=0}\end{array}\right.$有正整数解,求整数a的值.分析 首先解方程组,用含a的代数式表示出x、y.根据y有正整数解的情况,确定字母a的值.
解答 解:$\left\{\begin{array}{l}{2x+ay=16①}\\{x-2y=0②}\end{array}\right.$
由②,得x=2y③
把③代入①,得4y+ay=16
即(4+a)y=16
当a≠-4时,y=$\frac{16}{4+a}$
因为方程组有正整数解,所以a=12、4、0、-2、-3.
当a=12、4、0、-2、-3时,方程组有正整数解.
点评 本题考查了二元一次方程组的解法及正整数解的意义.解决本题的关键是把解用含a的代数式表示出来.

练习册系列答案
 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案
相关题目
17.钓鱼岛是中国的固有领土,面积约4400000平方米,数据4400000用科学记数法表示应为( )
| A. | 44×105 | B. | 0.44×107 | C. | 4.4×106 | D. | 4.4×105 |
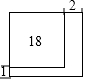 公园有一块正方形的空地,后来从这块空地上划出部分区域栽种鲜花(如图),原空地一边减少了1m,另一边减少了2m,剩余空地的面积为18m2,求原正方形空地的边长为6m(精确到1m)
公园有一块正方形的空地,后来从这块空地上划出部分区域栽种鲜花(如图),原空地一边减少了1m,另一边减少了2m,剩余空地的面积为18m2,求原正方形空地的边长为6m(精确到1m) 如图,一直线与两坐标轴的正半轴分别交于A,B两点,P是线段AB上任意一点(不包括端点).过点P分别作两坐标轴的垂线,且与两坐标轴围成的矩形的周长为10,则该直线的函数表达式是y=-x+5.
如图,一直线与两坐标轴的正半轴分别交于A,B两点,P是线段AB上任意一点(不包括端点).过点P分别作两坐标轴的垂线,且与两坐标轴围成的矩形的周长为10,则该直线的函数表达式是y=-x+5.



 如图,Rt△ABO中,∠OAB=Rt∠,点A在x轴的正半轴,点B在第一象限,函数y=$\frac{k}{x}$(k>0,x>0)的图象与边AB,OB分别交于点C,D,若S△BCD=1,S△OCD=2,则k的值为$\frac{24}{5}$.
如图,Rt△ABO中,∠OAB=Rt∠,点A在x轴的正半轴,点B在第一象限,函数y=$\frac{k}{x}$(k>0,x>0)的图象与边AB,OB分别交于点C,D,若S△BCD=1,S△OCD=2,则k的值为$\frac{24}{5}$.