��Ŀ����
20�����������У�����������У���������һ��ͼ�����۾���ƽ�ƻ�����ת���任���ͼ����ԭ��ͼ�εĶ�Ӧ�߶�һ��ƽ�У�
�ں���y=x2+$\frac{1}{\sqrt{-x}}$ͼ���ϵĵ�p��x��y��һ���ڵڶ����ޣ�
����ͶӰ��ͶӰ�߱˴�ƽ���Ҵ�ֱ��ͶӰ�棻
��ʹ��|x|-y=3��y+x2=0ͬʱ������x��ȡֵΪ$\frac{-1+\sqrt{13}}{2}$��
| A�� | 3�� | B�� | 1�� | C�� | 4�� | D�� | 2�� |
���� ������Ŀ�еĸ��������˵�������ж��Ƿ�Ϊ�����⣬������Խ����
��� �⣺һ��ͼ�����۾���ƽ�ƻ�����ת���任���ͼ����ԭ��ͼ�εĶ�Ӧ�߶���ȣ�����һ��ƽ�У��ʢ�Ϊ�����⣬
�ߺ���y=x2+$\frac{1}{\sqrt{-x}}$����x��0��y��0���ʺ���y=x2+$\frac{1}{\sqrt{-x}}$ͼ���ϵĵ�p��x��y��һ���ڵڶ����ޣ��ʢ�Ϊ�����⣬
��ͶӰ��ͶӰ�߱˴�ƽ���Ҵ�ֱ��ͶӰ�棬�ʢ�Ϊ�����⣬
$\left\{\begin{array}{l}{|x|-y=3}\\{y+{x}^{2}=0}\end{array}\right.$����$\left\{\begin{array}{l}{x=\frac{-1+\sqrt{13}}{2}}\\{y=\frac{-7+\sqrt{13}}{2}}\end{array}\right.$���ʢ��������⣬
��ѡA��
���� ���⿼�������붨���������Ĺؼ��ǿ����ж���Ŀ�и����������٣�

��ϰ��ϵ�д�
�����Ŀ
11�� ��ͼ��A��B����ֱ�λ��һ�����������ˣ�С���������Ӳ���A��B�ľ��룬�����Ӳ�����һλͬѧ��������һ�����⣺���ڵ���ȡһ������ֱ�ӴﵽA�ĵ�C���ҵ�AC��BC���е�D��E����������DE�ij�Ϊ15�ף���A��B�����ľ����ǣ�������
��ͼ��A��B����ֱ�λ��һ�����������ˣ�С���������Ӳ���A��B�ľ��룬�����Ӳ�����һλͬѧ��������һ�����⣺���ڵ���ȡһ������ֱ�ӴﵽA�ĵ�C���ҵ�AC��BC���е�D��E����������DE�ij�Ϊ15�ף���A��B�����ľ����ǣ�������
 ��ͼ��A��B����ֱ�λ��һ�����������ˣ�С���������Ӳ���A��B�ľ��룬�����Ӳ�����һλͬѧ��������һ�����⣺���ڵ���ȡһ������ֱ�ӴﵽA�ĵ�C���ҵ�AC��BC���е�D��E����������DE�ij�Ϊ15�ף���A��B�����ľ����ǣ�������
��ͼ��A��B����ֱ�λ��һ�����������ˣ�С���������Ӳ���A��B�ľ��룬�����Ӳ�����һλͬѧ��������һ�����⣺���ڵ���ȡһ������ֱ�ӴﵽA�ĵ�C���ҵ�AC��BC���е�D��E����������DE�ij�Ϊ15�ף���A��B�����ľ����ǣ�������| A�� | 15�� | B�� | 20�� | C�� | 30�� | D�� | 40�� |
8�� ��ͼ��һ�κ���y1=x����κ���y2�Tax2+bx+cͼ���ཻ��P��Q���㣬���ں���y3�Tax2+��b-1��x+c�������н��ۣ�
��ͼ��һ�κ���y1=x����κ���y2�Tax2+bx+cͼ���ཻ��P��Q���㣬���ں���y3�Tax2+��b-1��x+c�������н��ۣ�
��a+c��0����b��1���ۺ���y3��ͼ����x����������㶼���������ϣ�
���У���ȷ���۵ĸ����ǣ�������
 ��ͼ��һ�κ���y1=x����κ���y2�Tax2+bx+cͼ���ཻ��P��Q���㣬���ں���y3�Tax2+��b-1��x+c�������н��ۣ�
��ͼ��һ�κ���y1=x����κ���y2�Tax2+bx+cͼ���ཻ��P��Q���㣬���ں���y3�Tax2+��b-1��x+c�������н��ۣ���a+c��0����b��1���ۺ���y3��ͼ����x����������㶼���������ϣ�
���У���ȷ���۵ĸ����ǣ�������
| A�� | 0�� | B�� | 1�� | C�� | 2�� | D�� | 3�� |
10��-$\frac{1}{3}$���෴���ǣ�������
| A�� | -3 | B�� | $\frac{1}{3}$ | C�� | 3 | D�� | -$\frac{1}{3}$ |
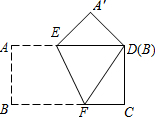 ��һ�ž���ֽƬABCD����ͼ��ʾ�ķ�ʽ�۵���ʹ����B��D�غϣ��ۺ�ΪEF��
��һ�ž���ֽƬABCD����ͼ��ʾ�ķ�ʽ�۵���ʹ����B��D�غϣ��ۺ�ΪEF��


