题目内容
3.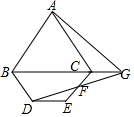 如图,等边三角形ABC中,AB=3,点D是△ABC外一点,连接BD,将线段BD绕点D顺时针旋转120°得到线段DE,连接CE,点F事CE的中点,射线DF与BC边的延长线交于点G,连接AG,若∠CBD=60°,∠ACE=90°,则线段AG的长为$\sqrt{13}$.
如图,等边三角形ABC中,AB=3,点D是△ABC外一点,连接BD,将线段BD绕点D顺时针旋转120°得到线段DE,连接CE,点F事CE的中点,射线DF与BC边的延长线交于点G,连接AG,若∠CBD=60°,∠ACE=90°,则线段AG的长为$\sqrt{13}$.
分析 过A作AH⊥BC于H,延长BD,CE交于M,解直角三角形得到AH=$\frac{3\sqrt{3}}{2}$,CH=$\frac{3}{2}$,根据平行线的判定定理得到BC∥DE,由平行线的性质得到∠EDF=∠CGF,根据全等三角形的性质得到CG=DE,由将线段BD绕点D顺时针旋转120°得到线段DE,得到BD=DE,根据三角形的内角和得到∠M=90°,根据平行线的性质得到∠DEM=30°,由直角三角形的性质得到DE=BD=2DM,根据勾股定理即可得到结论.
解答 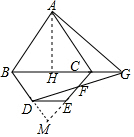 解:过A作AH⊥BC于H,延长BD,CE交于M,
解:过A作AH⊥BC于H,延长BD,CE交于M,
∵等边三角形ABC中,AB=3,
∴AH=$\frac{3\sqrt{3}}{2}$,CH=$\frac{3}{2}$,
∵∠BDE=120°,∠CBD=60°,
∴∠BDE+∠CBD=180°,
∴BC∥DE,
∴∠EDF=∠CGF,
∵点F是CE的中点,
∴DF=CF,
在△DEF与△GCF中,$\left\{\begin{array}{l}{∠EDF=∠CGF}\\{∠DFE=∠GFC}\\{EF=CF}\end{array}\right.$,
∴△DEF≌△GCF,
∴CG=DE,
∵将线段BD绕点D顺时针旋转120°得到线段DE,
∴BD=DE,
∴BD=DE=CG,
∵∠ACE=90°,∠ACB=60°,
∴∠BCE=30°,
∴∠M=90°,
∵DE∥BC,
∴∠DEM=30°,
∴DE=BD=2DM,
∴BD=$\frac{2}{3}$BM,
∵BC=3,
∴BM=$\frac{1}{2}$BC=$\frac{3}{2}$
∴BD=1,
∴CG=1,
∴HG=2.5,
∴AG=$\sqrt{A{H}^{2}+H{G}^{2}}$=$\sqrt{13}$.
故答案为:$\sqrt{13}$.
点评 本题考查了旋转的性质,全等三角形的判断和性质,勾股定理,等边三角形的性质,正确的作出辅助线是解题的关键.

 如图,已知正方形铁丝框ABCD边长为10,现使其变形为以A为圆心,AB为半径的扇形(忽略铁丝的粗细),则所得的扇形的面积为( )
如图,已知正方形铁丝框ABCD边长为10,现使其变形为以A为圆心,AB为半径的扇形(忽略铁丝的粗细),则所得的扇形的面积为( )| A. | 50 | B. | 100 | C. | 150 | D. | 200 |
 如图,A、B两点分别位于一个池塘的两端,小明想用绳子测量A,B的距离,但绳子不够,一位同学帮他想了一个主意:先在地上取一个可以直接达到A的点C,找到AC,BC的中点D,E,并且量得DE的长为15米,则A,B两点间的距离是( )
如图,A、B两点分别位于一个池塘的两端,小明想用绳子测量A,B的距离,但绳子不够,一位同学帮他想了一个主意:先在地上取一个可以直接达到A的点C,找到AC,BC的中点D,E,并且量得DE的长为15米,则A,B两点间的距离是( )| A. | 15米 | B. | 20米 | C. | 30米 | D. | 40米 |
 如图,一次函数y1=x与二次函数y2═ax2+bx+c图象相交于P,Q两点,对于函数y3═ax2+(b-1)x+c,有下列结论:
如图,一次函数y1=x与二次函数y2═ax2+bx+c图象相交于P,Q两点,对于函数y3═ax2+(b-1)x+c,有下列结论:①a+c>0;②b<1;③函数y3的图象与x轴的两个交点都在正半轴上;
其中,正确结论的个数是( )
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
 如图,已知a∥b,直角三角板的直角顶点在直线b上,若∠1=60°,则∠2等于( )
如图,已知a∥b,直角三角板的直角顶点在直线b上,若∠1=60°,则∠2等于( )| A. | 30° | B. | 40° | C. | 50° | D. | 60° |
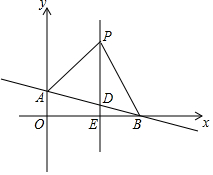 如图,在平面直角坐标系中,直线AB:y=kx+1(k≠0)交y轴于点A,交x轴于点B(3,0),平行于y轴的直线x=2交AB于点D,交x轴于点E,点P是直线x=2上一动点,且在点D的上方,设P(2,n).
如图,在平面直角坐标系中,直线AB:y=kx+1(k≠0)交y轴于点A,交x轴于点B(3,0),平行于y轴的直线x=2交AB于点D,交x轴于点E,点P是直线x=2上一动点,且在点D的上方,设P(2,n). 如图,一直线与两坐标轴的正半轴分别交于A,B两点,P是线段AB上任意一点(不包括端点).过点P分别作两坐标轴的垂线,且与两坐标轴围成的矩形的周长为10,则该直线的函数表达式是y=-x+5.
如图,一直线与两坐标轴的正半轴分别交于A,B两点,P是线段AB上任意一点(不包括端点).过点P分别作两坐标轴的垂线,且与两坐标轴围成的矩形的周长为10,则该直线的函数表达式是y=-x+5.


