题目内容
12.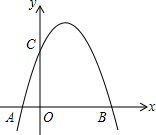 如图所示,在平面直角坐标系中,抛物线y=-$\frac{4}{3}{x}^{2}+bx+c$与x轴交于A、B两点,与y轴交于C点,其中B(3,0),C(0,4),点A在x轴的负半轴上.
如图所示,在平面直角坐标系中,抛物线y=-$\frac{4}{3}{x}^{2}+bx+c$与x轴交于A、B两点,与y轴交于C点,其中B(3,0),C(0,4),点A在x轴的负半轴上.(1)求抛物线的解析式和点A的坐标;
(2)连接AC、BC,设点P是x轴正半轴上一个动点,过点P作PM∥BC交射线AC于点M,连接CP,请探究是否存在使S△CPM=2的P点?若存在,请求出P点的坐标;若不存在,请简述理由.
分析 (1)用待定系数法确定抛物线解析式;
(2)先利用勾股定理求出AC,再判断出△AOC∽△AHP,表示出PH,再分点P在点B左侧和右侧两种情况讨论.
解答 解:(1)∵抛物线y=-$\frac{4}{3}{x}^{2}+bx+c$经过B(3,0).C(0,4),
∴$\left\{\begin{array}{l}{-\frac{4}{3}{x}^{2}+3b+3=0}\\{c=4}\end{array}\right.$,
∴$\left\{\begin{array}{l}{b=\frac{8}{3}}\\{c=4}\end{array}\right.$,
∴y=-$\frac{4}{3}$x2+$\frac{8}{3}$x+4,
设y=0,
∴-$\frac{4}{3}$x2+$\frac{8}{3}$x+4=0,
∴x1=3,x2=-1,
∵点A在x轴上,
∴A(-1,0);
(2)存在;如图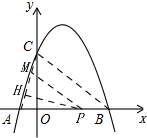
∵在Rt△AOC中,OA=1,OC=4,
∴AC=$\sqrt{17}$,
过点P作PH⊥AC,
∵P在x轴正半轴上,
∴设P(t,0),
∵A(-1,0),
∴PA=t+1,
∵∠AOC=∠PHA=90°,∠A=∠A,
∴△AOC∽△AHP,
∴$\frac{OC}{AC}$=$\frac{HP}{AP}$,
∴$\frac{4}{\sqrt{17}}=\frac{HP}{t+1}$,
∴PH=$\frac{4\sqrt{17}(t+1)}{17}$,
∵PM∥BC,$\frac{BP}{AB}=\frac{CM}{AC}$,
∵B(3,0),P(t,0),
当点P在点B左侧时,BP=3-t,
∴$\frac{3-t}{4}=\frac{CM}{\sqrt{17}}$,
∴CM=$\frac{\sqrt{17}(3-t)}{4}$,
∵S△PCM=2,
∴$\frac{1}{2}×\frac{\sqrt{17}(3-t)}{4}×\frac{4\sqrt{17}(t+1)}{17}=2$,
∴t=1,
∴P(1,0),
当点P在点B左侧时,BP=t-3,
∴$\frac{t-3}{4}=\frac{CM}{\sqrt{17}}$,
∴CM=$\frac{\sqrt{17}(t-3)}{4}$,
∴$\frac{1}{2}×\frac{\sqrt{17}(t-3)}{4}×\frac{4\sqrt{17}(t+1)}{17}=2$,
∴t=1±2$\sqrt{2}$,
∵点P是x轴正半轴上的一个动点,
∴P(1+2$\sqrt{2}$,0),
∴P点坐标为(1,0),(1+2$\sqrt{2}$,0).
点评 此题是二次函数综合题,主要考查了用待定系数法求解析式,相似三角形的判定和性质,用点P(t,0)中的t表示出CM,PH是解本题的关键,分点P在点B左和右两种情况是本题的难点.

| A. | 有两个相等的实根 | B. | 有实根 | ||
| C. | 有两个不相等的实根 | D. | 没有实根 |
| A. | x | B. | x-y | C. | -x(x-y) | D. | (x-m)(x-n) |
 如图所示的几何体是由六个小正方体组合而成的,它的左视图是( )
如图所示的几何体是由六个小正方体组合而成的,它的左视图是( )



 如图,某同学在楼房的A处测得荷塘的一端D处的俯角为60°,另一端B处的俯角为30°,荷塘另一端D与点C、B在同一直线上,已知楼高AC=24米,求荷塘宽BD为多少米?
如图,某同学在楼房的A处测得荷塘的一端D处的俯角为60°,另一端B处的俯角为30°,荷塘另一端D与点C、B在同一直线上,已知楼高AC=24米,求荷塘宽BD为多少米?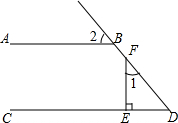 如图,AB∥CD,FE⊥CD,垂足为E,∠1=40°,则∠2的度数是50°.
如图,AB∥CD,FE⊥CD,垂足为E,∠1=40°,则∠2的度数是50°.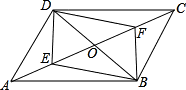 如图,在平行四边形ABCD中,对角线BD=12cm,AC=16cm,AC,BD相交于点O,若E,F是AC上两动点,分别从A,C两点以相同的速度向C、A运动,其速度为0.5cm/s.
如图,在平行四边形ABCD中,对角线BD=12cm,AC=16cm,AC,BD相交于点O,若E,F是AC上两动点,分别从A,C两点以相同的速度向C、A运动,其速度为0.5cm/s.