题目内容
18.已知二次函数y=ax2+bx+c的图象与x轴交于点(-2,0),(x1,0)且1<x1<2,与y轴正半轴的交点在(0,2)的下方,下列结论:①a<b<c;②b2-4ac>-8a;③4a+c<0;④2a-b+1<0.其中正确结论是(填写序号)①③.分析 采用形数结合的方法解题,根据抛物线的开口方向,对称轴的位置判断a、b、c的符号,把两根关系与抛物线与x的交点情况结合起来分析问题.
解答 解:①因为图象与x轴两交点为(-2,0),(x1,0),且1<x1<2,
对称轴x=$\frac{-2+{x}_{1}}{2}$=-$\frac{b}{2a}$,
则对称轴-$\frac{1}{2}$<-$\frac{b}{2a}$<0,且a<0,
∴a<b<0,
由抛物线与y轴的正半轴的交点在(0,2)的下方,得c>0,即a<b<c,①正确;
②假设b2-4ac>-8a成立,
由于a<0,所以4ac-b2<8a,
∴$\frac{4ac-{b}^{2}}{4a}$>2,
∴抛物线的顶点纵坐标应该大于2,
由题可知:抛物线与y轴的正半轴的交点在(0,2)的下方,抛物线的对称轴大于-1
∴顶点一定在这个交点的上方,但不代表顶点纵坐标应该大于2.
∴假设不成立,即②错误;
③设x2=-2,则x1x2=$\frac{c}{a}$,而1<x1<2,
∴-4<x1x2<-2,
∴-4<$\frac{c}{a}$<-2,
∴2a+c>0,4a+c<0.
∴③正确;
④抛物线过(-2,0),则4a-2b+c=0,而c<2,则4a-2b+2>0,即2a-b+1>0.④错误.
故答案为:①③.
点评 本题主要考查对二次函数图象上点的坐标特征,抛物线与X轴的交点,二次函数与系数的关系等知识点的理解和掌握,能根据图象确定与系数有关的式子的符号是解此题的关键.

练习册系列答案
相关题目
13.太阳的半径大约是696 000千米,用科学记数法可表示为( )
| A. | 696×103千米 | B. | 6.96×105千米 | C. | 6.96×106千米 | D. | 0.696×106千米 |
7.-x(x-y)(x-m)+xy(x-y)(x-n)的公因式是( )
| A. | x | B. | x-y | C. | -x(x-y) | D. | (x-m)(x-n) |
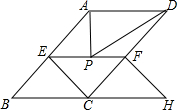 如图,在?ABCD中,AB=7,BC=5,sinB=$\frac{4}{5}$,将?ABCD折叠,使点A落在点C上,点D的对应点为H,折痕为EF.
如图,在?ABCD中,AB=7,BC=5,sinB=$\frac{4}{5}$,将?ABCD折叠,使点A落在点C上,点D的对应点为H,折痕为EF.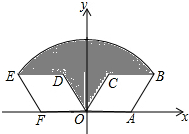 如图,菱形OABC的顶点A的坐标为(2,0),∠COA=60°,将菱形OABC绕坐标原点O逆时针旋转120°得到菱形ODEF,则线段OB=2$\sqrt{3}$;图中阴影部分的面积为4π-2$\sqrt{3}$.
如图,菱形OABC的顶点A的坐标为(2,0),∠COA=60°,将菱形OABC绕坐标原点O逆时针旋转120°得到菱形ODEF,则线段OB=2$\sqrt{3}$;图中阴影部分的面积为4π-2$\sqrt{3}$. 如图,某同学在楼房的A处测得荷塘的一端D处的俯角为60°,另一端B处的俯角为30°,荷塘另一端D与点C、B在同一直线上,已知楼高AC=24米,求荷塘宽BD为多少米?
如图,某同学在楼房的A处测得荷塘的一端D处的俯角为60°,另一端B处的俯角为30°,荷塘另一端D与点C、B在同一直线上,已知楼高AC=24米,求荷塘宽BD为多少米?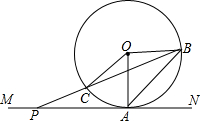 如图,MN是⊙O的切线,点A为切点,点P是射线AM上的任意一点.点B是⊙O上的一点,连接PB交⊙O于点C.
如图,MN是⊙O的切线,点A为切点,点P是射线AM上的任意一点.点B是⊙O上的一点,连接PB交⊙O于点C.