题目内容
9.解分式方程:(1)$\frac{1}{1-3x}$-$\frac{3}{2}$=$\frac{2}{3x-1}$
(2)$\frac{2}{x+3}$+$\frac{6}{{{x^2}-9}}$=$\frac{1}{x-3}$.
分析 两分式方程去分母转化为整式方程,求出整式方程的解得到x的值,经检验即可得到分式方程的解.
解答 解:(1)方程的两边同乘2(3x-1),得-2-3(3x-1)=4,
解得:x=-$\frac{1}{3}$.
检验:把x=-$\frac{1}{3}$代入2(3x-1)=-4≠0,
则原方程的解为:x=-$\frac{1}{3}$;
(2)去分母得:2(x-3)+6=x+3,
解得:x=3,
检验:把x=3代入(x-3)(x+3)=0,
则x=3是增根,原分式方程无解.
点评 此题考查了解分式方程,利用了转化的思想,解分式方程注意要检验.

练习册系列答案
相关题目
1.某工程队有14名员工,他们的工种及相应每人每月工资如下表所示:现该工稈队进行人员调整:减少木工2名,增加电工、瓦工各1名:与调整前相比,该工程队员工月工资的方差变大(填“变小”、“不变”或“变大”)
| 工种 | 人数 | 每人每月工资/元 |
| 电工 | 5 | 4000 |
| 木工 | 4 | 3000 |
| 瓦工 | 5 | 2000 |
18.实验中学团委举办了“中国梦,我的梦”演讲比赛,满分10分,学生得分均为整数,成绩达6分以上获优胜奖,达到9分以上获优秀奖.这次竞赛中初中、高中两组学生成绩分布的条形统计图如下:
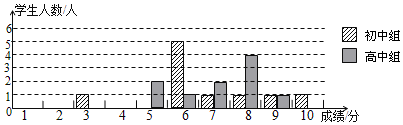
(1)补充完成下列的成绩统计分析表:
(2)安欣同学说:“这次竞赛我得了7分,在我们小组中排名属中游略偏上!”观察上表可知:安欣是初中组学生(填“初中”或“高中”);
(3)初中组同学说他们组的优胜奖率、优秀奖率均高于高中组,所以他们组的成绩好于高中组.但高中组同学不同意初中组同学的说法,认为他们组的成绩要好于初中组.请你给出两条支持高中组同学观点的理由.

(1)补充完成下列的成绩统计分析表:
| 组别 | 平均分 | 中位数 | 众数 | 方差 | 优胜奖率 | 优秀奖率 |
| 初中 | 6.7 | 6 | 6 | 3.41 | 90% | 20% |
| 高中 | 7.1 | 7.5 | 8 | 1.69 | 80% | 10% |
(3)初中组同学说他们组的优胜奖率、优秀奖率均高于高中组,所以他们组的成绩好于高中组.但高中组同学不同意初中组同学的说法,认为他们组的成绩要好于初中组.请你给出两条支持高中组同学观点的理由.
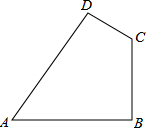 如图,已知四边形ABCD中,AB=20cm,BC=15cm,CD=7cm,AD=24cm,∠ABC=90°.猜想∠A与∠C关系是互补.
如图,已知四边形ABCD中,AB=20cm,BC=15cm,CD=7cm,AD=24cm,∠ABC=90°.猜想∠A与∠C关系是互补.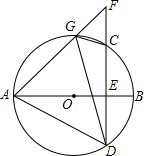 如图,AB是⊙O直径,弦CD⊥AB于点E,G是弧AC上任意一点,延长AG,与DC的延长线相交于点F,连结AD,GD,CG,则与∠AGD相等的角有( )
如图,AB是⊙O直径,弦CD⊥AB于点E,G是弧AC上任意一点,延长AG,与DC的延长线相交于点F,连结AD,GD,CG,则与∠AGD相等的角有( ) 如图,AB为⊙O的直径,C为⊙O上一点,弦AD平分∠BAC,交BC于点E,AB=5,AD=4,则AE的长为$\frac{4}{7}$.
如图,AB为⊙O的直径,C为⊙O上一点,弦AD平分∠BAC,交BC于点E,AB=5,AD=4,则AE的长为$\frac{4}{7}$.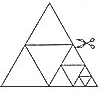 如图,将一张等边三角形纸片沿任意两边中点的连线可剪成4个小三角形,称为第一次操作;然后,将其中的一个三角形按同样方式再剪成4个小三角形,共得到7个小三角形,称为第二次操作;再将其中一个三角形按同样方式再剪成4个小三角形,共得到10个小三角形,称为第三次操作:…,根据以上操作,若操作的次数是n时,则可得到的小三角形个数为( )
如图,将一张等边三角形纸片沿任意两边中点的连线可剪成4个小三角形,称为第一次操作;然后,将其中的一个三角形按同样方式再剪成4个小三角形,共得到7个小三角形,称为第二次操作;再将其中一个三角形按同样方式再剪成4个小三角形,共得到10个小三角形,称为第三次操作:…,根据以上操作,若操作的次数是n时,则可得到的小三角形个数为( )