题目内容
19.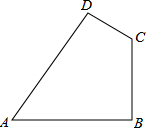 如图,已知四边形ABCD中,AB=20cm,BC=15cm,CD=7cm,AD=24cm,∠ABC=90°.猜想∠A与∠C关系是互补.
如图,已知四边形ABCD中,AB=20cm,BC=15cm,CD=7cm,AD=24cm,∠ABC=90°.猜想∠A与∠C关系是互补.
分析 连接AC,然后根据勾股定理求出AC的值,然后根据勾股定理的逆定理判断△ADC为Rt△,然后根据四边形的内角和定理即可得到∠A与∠C关系.
解答 解:∠A与∠C关系为:互补.理由如下:
连结AC,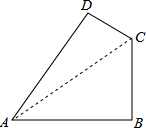
∵∠ABC=90°,
∴在Rt△ABC中,由勾股定理得:
AC=$\sqrt{A{B}^{2}+B{C}^{2}}$=25cm,
∵AD2+DC2=625=252=AC2,
∴△ADC是直角三角形,且∠D=90°,
∵∠DAB+∠B+∠BCD+∠D=180°,
∴∠DAB+∠BCD=180°,
即∠A+∠C=180°,
故答案为:互补.
点评 此题考查了勾股定理及勾股定理的逆定理,解题的关键是:根据勾股定理的逆定理判断△ADC是直角三角形.

练习册系列答案
相关题目
1.如图:∠1和∠2是同位角的是( )


| A. | ②③ | B. | ①②③ | C. | ①②④ | D. | ①④ |
 有一塔形几何体由若干个正方体构成,构成方式如图所示,上层正方体下底面的四个顶点是下层正方体上底面各边的中点.已知最底层正方体的棱长为2,且该塔形的表面积(含最底层正方体的底面面积)超过39,则该塔形中正方体的个数至少是6.
有一塔形几何体由若干个正方体构成,构成方式如图所示,上层正方体下底面的四个顶点是下层正方体上底面各边的中点.已知最底层正方体的棱长为2,且该塔形的表面积(含最底层正方体的底面面积)超过39,则该塔形中正方体的个数至少是6.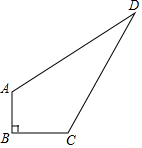 如图,在四边形ABCD中,已知AB=3,BC=4,CD=12,AD=13,∠B=90°.求四边形ABCD的面积.
如图,在四边形ABCD中,已知AB=3,BC=4,CD=12,AD=13,∠B=90°.求四边形ABCD的面积. 如图,在四边形ABCD中,∠A=90°,AD=3,AB=4,BC=12,CD=13,试判断△BCD的形状,并说明理由.
如图,在四边形ABCD中,∠A=90°,AD=3,AB=4,BC=12,CD=13,试判断△BCD的形状,并说明理由. 如图,AB是⊙O的直径,C,D在⊙O上,CD=AD,分别延长CD、BA相交于点E,且AE=$\sqrt{2}$OA,若BC=6,求⊙O的半径.
如图,AB是⊙O的直径,C,D在⊙O上,CD=AD,分别延长CD、BA相交于点E,且AE=$\sqrt{2}$OA,若BC=6,求⊙O的半径.