题目内容
17.关于x的方程m(x+h)2+k=0(m,h,k均为常数,m≠0)的解是x1=-3,x2=2,则方程m(x+h-3)2+k=0的解为x=0或x=5.分析 利用直接开平方法得方程m(x+h)2+k=0的解x=-h±$\sqrt{\frac{k}{m}}$,则-h-$\sqrt{\frac{k}{m}}$=-3,-h+$\sqrt{\frac{k}{m}}$=2,再解方程m(x+h-3)2+k=0得x=3-h±$\sqrt{\frac{k}{m}}$,所以x1=0,x2=5.
解答 解:解方程m(x+h)2+k=0(m,h,k均为常数,m≠0)得x=-h±$\sqrt{\frac{k}{m}}$,
而关于x的方程m(x+h)2+k=0(m,h,k均为常数,m≠0)的解是x1=-3,x2=2,
所以-h-$\sqrt{\frac{k}{m}}$=-3,-h+$\sqrt{\frac{k}{m}}$=2,
方程m(x+h-3)2+k=0的解为x=3-h±$\sqrt{\frac{k}{m}}$,
所以x1=3-3=0,x2=3+2=5.
故答案为:x=0或x=5.
点评 本题考查了解一元二次方程-直接开平方法:形如x2=p或(nx+m)2=p(p≥0)的一元二次方程可采用直接开平方的方法解一元二次方程.如果方程化成x2=p的形式,那么可得x=±$\sqrt{p}$;如果方程能化成(nx+m)2=p(p≥0)的形式,那么nx+m=±$\sqrt{p}$.

练习册系列答案
相关题目
5. 如图,⊙O半径为3,Rt△ABC的顶点A,B在⊙O上,∠A=30°,点C在⊙O内,当点A在圆上运动时,OC的最小值为( )
如图,⊙O半径为3,Rt△ABC的顶点A,B在⊙O上,∠A=30°,点C在⊙O内,当点A在圆上运动时,OC的最小值为( )
 如图,⊙O半径为3,Rt△ABC的顶点A,B在⊙O上,∠A=30°,点C在⊙O内,当点A在圆上运动时,OC的最小值为( )
如图,⊙O半径为3,Rt△ABC的顶点A,B在⊙O上,∠A=30°,点C在⊙O内,当点A在圆上运动时,OC的最小值为( )| A. | $\sqrt{2}$ | B. | $\frac{3}{2}$ | C. | $\sqrt{3}$ | D. | 2 |
 有一塔形几何体由若干个正方体构成,构成方式如图所示,上层正方体下底面的四个顶点是下层正方体上底面各边的中点.已知最底层正方体的棱长为2,且该塔形的表面积(含最底层正方体的底面面积)超过39,则该塔形中正方体的个数至少是6.
有一塔形几何体由若干个正方体构成,构成方式如图所示,上层正方体下底面的四个顶点是下层正方体上底面各边的中点.已知最底层正方体的棱长为2,且该塔形的表面积(含最底层正方体的底面面积)超过39,则该塔形中正方体的个数至少是6.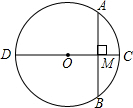 如图,⊙O的直径CD=10,AB是⊙O的弦,AB⊥CD,垂足为M,OM:OC=3:5.求AB的长度.
如图,⊙O的直径CD=10,AB是⊙O的弦,AB⊥CD,垂足为M,OM:OC=3:5.求AB的长度.
 已知函数y=ax+b的大致图象如图所示,那么二次函数y=ax2+bx+1的图象可能是( )
已知函数y=ax+b的大致图象如图所示,那么二次函数y=ax2+bx+1的图象可能是( )


