题目内容
19.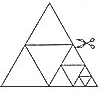 如图,将一张等边三角形纸片沿任意两边中点的连线可剪成4个小三角形,称为第一次操作;然后,将其中的一个三角形按同样方式再剪成4个小三角形,共得到7个小三角形,称为第二次操作;再将其中一个三角形按同样方式再剪成4个小三角形,共得到10个小三角形,称为第三次操作:…,根据以上操作,若操作的次数是n时,则可得到的小三角形个数为( )
如图,将一张等边三角形纸片沿任意两边中点的连线可剪成4个小三角形,称为第一次操作;然后,将其中的一个三角形按同样方式再剪成4个小三角形,共得到7个小三角形,称为第二次操作;再将其中一个三角形按同样方式再剪成4个小三角形,共得到10个小三角形,称为第三次操作:…,根据以上操作,若操作的次数是n时,则可得到的小三角形个数为( )| A. | 3n-1 | B. | 3(n-1) | C. | 3(n+1) | D. | 3n+1 |
分析 由第一次操作后三角形共有4个、第二次操作后三角形共有(4+3)个、第三次操作后三角形共有(4+3+3)个,可得第n次操作后三角形共有4+3(n-1)=3n+1个;
解答 解:∵第一次操作后,三角形共有4个;
第二次操作后,三角形共有4+3=7个;
第三次操作后,三角形共有4+3+3=10个;
…
∴第n次操作后,三角形共有4+3(n-1)=3n+1个;
故选D.
点评 此题主要考查了图形的变化类问题以及三角形中位线定理的运用,根据已知得出第n次操作后,三角形的个数为3n+1是解题关键.

练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案
相关题目
10.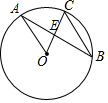 如图,已知⊙O的半径为2,点A、B、C为圆上三点,且OA∥BC,则$\frac{1}{CE}-\frac{1}{BC}$的值是( )
如图,已知⊙O的半径为2,点A、B、C为圆上三点,且OA∥BC,则$\frac{1}{CE}-\frac{1}{BC}$的值是( )
 如图,已知⊙O的半径为2,点A、B、C为圆上三点,且OA∥BC,则$\frac{1}{CE}-\frac{1}{BC}$的值是( )
如图,已知⊙O的半径为2,点A、B、C为圆上三点,且OA∥BC,则$\frac{1}{CE}-\frac{1}{BC}$的值是( )| A. | 2 | B. | $\frac{1}{2}$ | C. | $\frac{3}{2}$ | D. | $\frac{2}{3}$ |
9.已知a<b,则下列式子中成立的是( )
| A. | a+3>b+3 | B. | 3-a>3-b | C. | a-3>b-3 | D. | -3a<-3b |
 已知函数y=ax+b的大致图象如图所示,那么二次函数y=ax2+bx+1的图象可能是( )
已知函数y=ax+b的大致图象如图所示,那么二次函数y=ax2+bx+1的图象可能是( )



