题目内容
4. 如图,AB为⊙O的直径,C为⊙O上一点,弦AD平分∠BAC,交BC于点E,AB=5,AD=4,则AE的长为$\frac{4}{7}$.
如图,AB为⊙O的直径,C为⊙O上一点,弦AD平分∠BAC,交BC于点E,AB=5,AD=4,则AE的长为$\frac{4}{7}$.
分析 连接BD、CD,由勾股定理先求出BD的长,再利用△ABD∽△BED,得出$\frac{DE}{DB}$=$\frac{DB}{AD}$,可解得DE的长,由AE=AD-DE求解即可得出答案.
解答 解:如图1,连接BD、CD,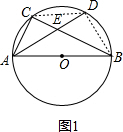 ,
,
∵AB为⊙O的直径,
∴∠ADB=90°,
∴BD=$\sqrt{A{B}^{2}-A{D}^{2}}$=3,
∵弦AD平分∠BAC,
∴CD=BD=3,
∴∠CBD=∠DAB,
∵∠BAD=∠EBD,∠ADB=∠BDE,
∴△ABD∽△BED,
∴$\frac{DE}{DB}$=$\frac{DB}{AD}$,即$\frac{DE}{3}$=$\frac{3}{4}$,
解得DE=$\frac{9}{4}$,
∴AE=AD-DE=4-$\frac{9}{4}$=$\frac{7}{4}$.
故答案为:$\frac{7}{4}$.
点评 此题主要考查了三角形相似的判定和性质及圆周角定理,解答此题的关键是得出△ABD∽△BED.

练习册系列答案
相关题目
16.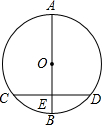 如图,AB是⊙O的直径,弦CD⊥AB于E,CD=16,EB=4,则AE=( )
如图,AB是⊙O的直径,弦CD⊥AB于E,CD=16,EB=4,则AE=( )
 如图,AB是⊙O的直径,弦CD⊥AB于E,CD=16,EB=4,则AE=( )
如图,AB是⊙O的直径,弦CD⊥AB于E,CD=16,EB=4,则AE=( )| A. | 20 | B. | 18 | C. | 16 | D. | 14 |
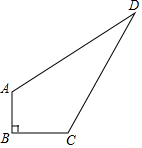 如图,在四边形ABCD中,已知AB=3,BC=4,CD=12,AD=13,∠B=90°.求四边形ABCD的面积.
如图,在四边形ABCD中,已知AB=3,BC=4,CD=12,AD=13,∠B=90°.求四边形ABCD的面积. 如图,四边形ABCD中∠A=90°,AB=3cm,AD=4cm,BC=13cm,CD=12cm,求四边形ABCD的面积?
如图,四边形ABCD中∠A=90°,AB=3cm,AD=4cm,BC=13cm,CD=12cm,求四边形ABCD的面积? 如图,在矩形ABCD中,点O在对角线AC上,以OA的半径的⊙O与AD、AC分别交于点E、F,且∠ACB=∠DCE.若tan∠ACB=$\frac{{\sqrt{2}}}{2}$,BC=2,则⊙O的半径为$\frac{\sqrt{6}}{4}$.
如图,在矩形ABCD中,点O在对角线AC上,以OA的半径的⊙O与AD、AC分别交于点E、F,且∠ACB=∠DCE.若tan∠ACB=$\frac{{\sqrt{2}}}{2}$,BC=2,则⊙O的半径为$\frac{\sqrt{6}}{4}$.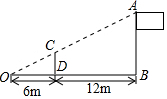 如图,小明用长为2.5m的竹竿CD做测量工具,测量学校旗杆AB的高度,移动竹竿,使竹竿、旗杆的顶端的影子恰好落在地面的同一点O.此时,竹竿与这一点O相距6m、与旗杆相距12m,则旗杆AB的高为7.5m.
如图,小明用长为2.5m的竹竿CD做测量工具,测量学校旗杆AB的高度,移动竹竿,使竹竿、旗杆的顶端的影子恰好落在地面的同一点O.此时,竹竿与这一点O相距6m、与旗杆相距12m,则旗杆AB的高为7.5m.