题目内容
 如图,在Rt△ABC中,∠BAC=90°,∠B=60°,BC=16cm,AD是斜边BC上的高,垂足为D,BE=1cm.点M从点B出发沿BC方向以1cm/s的速度运动,点N从点E出发,与点M同时同方向以相同的速度运动,以MN为边在BC的上方作正方形MNGH.点M到达点D时停止运动,点N到达点C时停止运动.设运动时间为t(s).
如图,在Rt△ABC中,∠BAC=90°,∠B=60°,BC=16cm,AD是斜边BC上的高,垂足为D,BE=1cm.点M从点B出发沿BC方向以1cm/s的速度运动,点N从点E出发,与点M同时同方向以相同的速度运动,以MN为边在BC的上方作正方形MNGH.点M到达点D时停止运动,点N到达点C时停止运动.设运动时间为t(s).(1)当t为何值时,点G刚好落在线段AD上?
(2)设正方形MNGH与Rt△ABC重叠部分的图形的面积为S,当重叠部分的图形是正方形时,求出S关于t的函数关系式并写出自变量t的取值范围.
(3)设正方形MNGH的边NG所在直线与线段AC交于点P,连接DP,当t为何值时,△CPD是等腰三角形?
考点:相似形综合题,勾股定理
专题:几何综合题
分析:(1)求出ED的距离即可求出相对应的时间t;
(2)先求出t的取值范围,分为H在AB上时,此时BM的距离,进而求出相应的时间.同样当G在AC上时,求出MN的长度,继而算出EN的长度即可求出时间,再通过正方形的面积公式求出正方形的面积;
(3)分两种情况,分别是DP=PC时和DC=PC时,分别EN的长度便可求出t的值.
(2)先求出t的取值范围,分为H在AB上时,此时BM的距离,进而求出相应的时间.同样当G在AC上时,求出MN的长度,继而算出EN的长度即可求出时间,再通过正方形的面积公式求出正方形的面积;
(3)分两种情况,分别是DP=PC时和DC=PC时,分别EN的长度便可求出t的值.
解答:解:由∠BAC=90°,∠B=60°,BC=16cm
易知:AB=8cm,BD=4cm,AC=8
cm,DC=12cm,AD=4
cm.
(1)∵当G刚好落在线段AD上时,ED=BD-BE=3cm
∴t=
s=3s.
(2)∵当MH没有到达AD时,此时正方形MNGH是边长为1的正方形,令H点在AB上,则
∠HMB=90°,∠B=60°,MH=1
∴BM=
cm
∴t=
s
当MH到达AD时,那么此时的正方形MNGH的边长随着N点的继续运动而增大,令G点在AC上,
设MN=xcm,则GH=DH=x,AH=
x,
∵AD=AH+DH=
x+x=4
,
∴x=6
-3.
当
≤t≤4时,SMNGH=1cm2
当4<t≤6
-3时,SMNGH=(t-3)2cm2
故S关于t的函数关系式为:
S=
.
(3)分两种情况:
①∵当DP=PC时,易知此时N点为DC的中点,
∴MN=6cm
∴EN=3cm+6cm=9cm
∴t=9s
故当t=9s的时候,△CPD为等腰三角形;
②当DC=PC时,DC=PC=12cm
∴NC=6
cm
∴EN=16cm-1cm-6
cm=(15-6
)cm
∴t=(15-6
)s
故当t=(15-6
)s时,△CPD为等腰三角形.
综上所述,当t=9s或t=(15-6
)s时,△CPD为等腰三角形.
易知:AB=8cm,BD=4cm,AC=8
| 3 |
| 3 |
(1)∵当G刚好落在线段AD上时,ED=BD-BE=3cm
∴t=
| 3 |
| 1 |
(2)∵当MH没有到达AD时,此时正方形MNGH是边长为1的正方形,令H点在AB上,则
∠HMB=90°,∠B=60°,MH=1
∴BM=
| ||
| 3 |
∴t=
| ||
| 3 |
当MH到达AD时,那么此时的正方形MNGH的边长随着N点的继续运动而增大,令G点在AC上,
设MN=xcm,则GH=DH=x,AH=
| ||
| 3 |
∵AD=AH+DH=
| ||
| 3 |
| 3 |
∴x=6
| 3 |
当
| ||
| 3 |
当4<t≤6
| 3 |
故S关于t的函数关系式为:
S=
|
(3)分两种情况:
①∵当DP=PC时,易知此时N点为DC的中点,
∴MN=6cm
∴EN=3cm+6cm=9cm
∴t=9s
故当t=9s的时候,△CPD为等腰三角形;
②当DC=PC时,DC=PC=12cm
∴NC=6
| 3 |
∴EN=16cm-1cm-6
| 3 |
| 3 |
∴t=(15-6
| 3 |
故当t=(15-6
| 3 |
综上所述,当t=9s或t=(15-6
| 3 |
点评:本题充分考查了学生对相似三角形和勾股定理的理解和运用,此题涉及到的知识点较多,有勾股定理.正方形的性质,相似三角形的判定与性质,综合性较强,利用学生系统的掌握知识,是一道好题.

练习册系列答案
相关题目
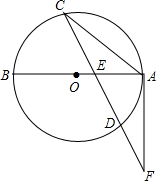 如图,已知AB是⊙O的直径,弦CD与AB交于点E,F为CD的延长线上一点,连接AF,且FA2=FD•FC.
如图,已知AB是⊙O的直径,弦CD与AB交于点E,F为CD的延长线上一点,连接AF,且FA2=FD•FC.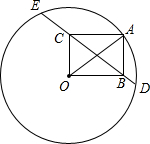 如图,⊙O的半径为20,A是⊙O上一点.以OA为对角线作矩形OBAC,且OC=12.延长BC,与⊙O分别交于D,E两点,则CE-BD的值等于
如图,⊙O的半径为20,A是⊙O上一点.以OA为对角线作矩形OBAC,且OC=12.延长BC,与⊙O分别交于D,E两点,则CE-BD的值等于