题目内容
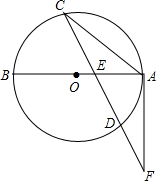 如图,已知AB是⊙O的直径,弦CD与AB交于点E,F为CD的延长线上一点,连接AF,且FA2=FD•FC.
如图,已知AB是⊙O的直径,弦CD与AB交于点E,F为CD的延长线上一点,连接AF,且FA2=FD•FC.(1)求证:FA为⊙O的切线;
(2)若AC=8,CE:ED=6:5,AE:EB=2:3,求AB的值.
考点:切线的判定,相似三角形的判定与性质
专题:综合题
分析:(1)连接BD、AD,由FA2=FD•FC可以证到△FAD∽△FCA,从而得到∠DAF=∠C,然后运用圆周角定理就可解决问题.
(2)设CE=6x,AE=2y,则ED=5x,EB=3y,由相交弦定理得:EC•ED=EB•EA,从而得到y=
x.由AF2=EF2-AE2=FD•FC可以得到DF=5x,从而有AD=ED=DF=5x.由△FAD∽△FCA得到
=
,从而可以求出x,进而求出AB的值.
(2)设CE=6x,AE=2y,则ED=5x,EB=3y,由相交弦定理得:EC•ED=EB•EA,从而得到y=
| 5 |
| AD |
| AC |
| DF |
| AF |
解答:(1)证明:连接BD、AD,如图,
∵FA2=FD•FC,
∴
=
.
∵∠F=∠F,
∴△FAD∽△FCA.
∴∠DAF=∠C.
∵∠DBA=∠C,
∴∠DBA=∠DAF.
∵AB是⊙O的直径,
∴∠ADB=90°.
∴∠DBA+∠DAB=90°.
∴∠DAF+∠DAB=90°.
∴∠FAB=90°,即AF⊥AB.
∴FA为⊙O的切线.
(2)解:设CE=6x,AE=2y,则ED=5x,EB=3y.
由相交弦定理得:EC•ED=EB•EA.
∴30x2=6y2.
∴y=
x.
∴AE=2
x.
∵∠FAB=90°,
∴AF2=EF2-AE2.
∴FD•FC=EF2-AE2.
∴FD•(FD+11x)=(FD+5x)2-(2
x)2.
∴FD=5x.
∴AF2=FD•FC=80x2.
∴AF=4
x.
∵∠FAE=90°,FD=ED=5x,
∴AD=ED=5x.
∵△FAD∽△FCA.
∴
=
.
∵AD=DF=5x,AC=8,AF=4
x,
∴
=
.
解得:x=
.
∴AB=5y=5
x=10.
∴AB的值为10.
∵FA2=FD•FC,
∴
| FA |
| FD |
| FC |
| FA |
∵∠F=∠F,
∴△FAD∽△FCA.
∴∠DAF=∠C.
∵∠DBA=∠C,
∴∠DBA=∠DAF.
∵AB是⊙O的直径,
∴∠ADB=90°.
∴∠DBA+∠DAB=90°.
∴∠DAF+∠DAB=90°.

∴∠FAB=90°,即AF⊥AB.
∴FA为⊙O的切线.
(2)解:设CE=6x,AE=2y,则ED=5x,EB=3y.
由相交弦定理得:EC•ED=EB•EA.
∴30x2=6y2.
∴y=
| 5 |
∴AE=2
| 5 |
∵∠FAB=90°,
∴AF2=EF2-AE2.
∴FD•FC=EF2-AE2.
∴FD•(FD+11x)=(FD+5x)2-(2
| 5 |
∴FD=5x.
∴AF2=FD•FC=80x2.
∴AF=4
| 5 |
∵∠FAE=90°,FD=ED=5x,
∴AD=ED=5x.
∵△FAD∽△FCA.
∴
| AD |
| AC |
| DF |
| AF |
∵AD=DF=5x,AC=8,AF=4
| 5 |
∴
| 5x |
| 8 |
| 5x | ||
4
|
解得:x=
2
| ||
| 5 |
∴AB=5y=5
| 5 |
∴AB的值为10.
点评:本题考查了相似三角形的判定与性质、切线的判定、相交弦定理、圆周角定理、勾股定理、直角三角形斜边上的中线等于斜边的一半等知识,有一定的难度,而利用AF2=FD•FC=EF2-AE2求出x是解决第二小题的关键.

练习册系列答案
 小学能力测试卷系列答案
小学能力测试卷系列答案
相关题目

 如图,在Rt△ABC中,∠BAC=90°,∠B=60°,BC=16cm,AD是斜边BC上的高,垂足为D,BE=1cm.点M从点B出发沿BC方向以1cm/s的速度运动,点N从点E出发,与点M同时同方向以相同的速度运动,以MN为边在BC的上方作正方形MNGH.点M到达点D时停止运动,点N到达点C时停止运动.设运动时间为t(s).
如图,在Rt△ABC中,∠BAC=90°,∠B=60°,BC=16cm,AD是斜边BC上的高,垂足为D,BE=1cm.点M从点B出发沿BC方向以1cm/s的速度运动,点N从点E出发,与点M同时同方向以相同的速度运动,以MN为边在BC的上方作正方形MNGH.点M到达点D时停止运动,点N到达点C时停止运动.设运动时间为t(s).