题目内容
14. 如图,在平面直角坐标系中,二次函数y=ax2+c(a≠0)的图象过面积为$\frac{1}{2}$的正方形ABOC的三个顶点A、B、C,则a的值为-2.
如图,在平面直角坐标系中,二次函数y=ax2+c(a≠0)的图象过面积为$\frac{1}{2}$的正方形ABOC的三个顶点A、B、C,则a的值为-2.
分析 要求出a的值,就是要求出二次函数的解析式.要求解析式就要求出A、B、C三点的坐标,要求坐标根据正方形的性质就可以解决问题而求出结果.
解答 解:作BD⊥x轴于点D,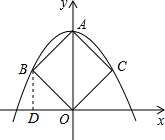
∴∠BDO=90°,
∵四边形ABOC是正方形,面积为$\frac{1}{2}$,
∴AB=BO=CO=AC=$\frac{\sqrt{2}}{2}$,∠AOB=45°,
∴∠BOD=∠DBO=45°,
∴BD=DO,
在Rt△ABO和Rt△BDO中由勾股定理得
AO=1,BD=DO=$\frac{1}{2}$,
∴A(0,1),B(-$\frac{1}{2}$,$\frac{1}{2}$),
∴$\left\{\begin{array}{l}{c=1}\\{\frac{1}{4}a+c=\frac{1}{2}}\end{array}\right.$,解得:$\left\{\begin{array}{l}{a=-2}\\{c=1}\end{array}\right.$
故答案为-2.
点评 本题是一道二次函数的综合题,考查了正方形的性质、勾股定理的运用,待定系数法求函数解析式的系数的方法.

练习册系列答案
相关题目
15.代数式$\frac{a}{\sqrt{{a}^{2}}}$$+\frac{b}{\sqrt{{b}^{2}}}$$+\frac{c}{\sqrt{{c}^{2}}}$的所有可能的值有( )
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 无数个 |
19.下列运算中,正确的是( )
| A. | 2a+3b=5ab | B. | 3x2÷2x=x | C. | (x2)3=x6 | D. | (x+y2)2=x2+y4 |
6. 如图,在△ABC中,AB=AC,过点A作AD∥BC,若∠1=65°,则∠BAC的大小为( )
如图,在△ABC中,AB=AC,过点A作AD∥BC,若∠1=65°,则∠BAC的大小为( )
 如图,在△ABC中,AB=AC,过点A作AD∥BC,若∠1=65°,则∠BAC的大小为( )
如图,在△ABC中,AB=AC,过点A作AD∥BC,若∠1=65°,则∠BAC的大小为( )| A. | 45° | B. | 50° | C. | 60° | D. | 65° |
 如图,抛物线y=ax2+bx过点A(4,0),正方形 OABC的边BC与抛物线的一个交点为D,点D的横坐标为3,点M在y轴负半轴上,直线l过点D、M两点且与抛物线的对称轴交于点H,tan∠OMD=$\frac{1}{3}$.
如图,抛物线y=ax2+bx过点A(4,0),正方形 OABC的边BC与抛物线的一个交点为D,点D的横坐标为3,点M在y轴负半轴上,直线l过点D、M两点且与抛物线的对称轴交于点H,tan∠OMD=$\frac{1}{3}$.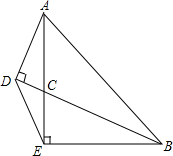 如图,△ABE中,∠AEB=90°,AE=BE,BC平分∠ABE交AE于C,AD⊥BC于D,连DE.
如图,△ABE中,∠AEB=90°,AE=BE,BC平分∠ABE交AE于C,AD⊥BC于D,连DE. 如图,△OBC为等边三角形,AD∥BC,AD=3,BC=7,P为BC边上一点(不与B,C重合),过点P作∠APE=∠B,PE交CD于E.
如图,△OBC为等边三角形,AD∥BC,AD=3,BC=7,P为BC边上一点(不与B,C重合),过点P作∠APE=∠B,PE交CD于E.