题目内容
2.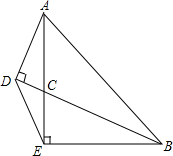 如图,△ABE中,∠AEB=90°,AE=BE,BC平分∠ABE交AE于C,AD⊥BC于D,连DE.
如图,△ABE中,∠AEB=90°,AE=BE,BC平分∠ABE交AE于C,AD⊥BC于D,连DE.(1)求证:BC=2AD;
(2)求证:AB=AE+CE;
(3)求证:∠EDB=45°.
分析 (1)延长AD、BE交于F点,由ASA证明△ABD≌△FBD,得出AD=FD=$\frac{1}{2}$AF,证出∠FAE=∠CBE,由AAS证明△AFE≌△BCE,得出AF=BC,即可得出结论;
(2)由全等三角形的性质得出FE=CE,由FB=FE+BE,BE=AE,即可得出AB=AE+CE;
(3)证出A、B、E、D四点共圆,由圆周角定理即可得出∠EDB=∠BAE=45°,
解答 (1)证明:延长AD、BE交于F点,如图所示: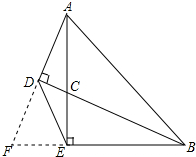
∵BD⊥AD且BD平分∠ABC,
∴∠ADB=∠FDB=90°,∠ABD=∠FBD,
在△ABD和△FBD中,$\left\{\begin{array}{l}{∠ADB=∠FDB}&{\;}\\{BD=BD}&{\;}\\{∠ABD=∠∠FBD}&{\;}\end{array}\right.$,
∴△ABD≌△FBD(ASA),
∴AD=FD=$\frac{1}{2}$AF,
∵∠FAE+∠F=90°,∠CBE+∠F=90°,
∴∠FAE=∠CBE,
∵在△AFE与△BCE中,$\left\{\begin{array}{l}{∠FAE=∠CBE}&{\;}\\{∠AEF=∠AEB=90°}&{\;}\\{AE=BE}&{\;}\end{array}\right.$,
∴△AFE≌△BCE(AAS),
∴AF=BC,
∴BC=2AD;
(2)证明:∵AD=FD,BD⊥AD,
∴AB=FB,由(1)得:△AFE≌△BCE,
∴FE=CE,
∵FB=FE+BE,BE=AE,
∴AB=AE+CE;
(3)证明:∵∠ADB=∠AEB=90°,AE=BE,
∴A、B、E、D四点共圆,∠BAE=45°,
∴∠EDB=∠BAE=45°.
点评 本题考查了全等三角形的判定与性质、等腰三角形的判定与性质、线段垂直平分线的性质、四点共圆、圆周角定理等知识;本题综合性强,有一定难度,证明三角形全等是解决问题的关键.

| A. | 32.5元 | B. | 33元 | C. | 40元 | D. | 38元 |
 已知AC、BD交于E,∠A=∠B,∠1=∠2,求证:AE=BE.
已知AC、BD交于E,∠A=∠B,∠1=∠2,求证:AE=BE. 如图,BE⊥AC、CF⊥AB于点E、F,BE与CF交于点D,DE=DF,连接AD.
如图,BE⊥AC、CF⊥AB于点E、F,BE与CF交于点D,DE=DF,连接AD. 如图,P是正三角形ABC内的一点,若将△PAC绕点A逆时针旋转后,得到△P′AB,
如图,P是正三角形ABC内的一点,若将△PAC绕点A逆时针旋转后,得到△P′AB, 如图,在平面直角坐标系中,二次函数y=ax2+c(a≠0)的图象过面积为$\frac{1}{2}$的正方形ABOC的三个顶点A、B、C,则a的值为-2.
如图,在平面直角坐标系中,二次函数y=ax2+c(a≠0)的图象过面积为$\frac{1}{2}$的正方形ABOC的三个顶点A、B、C,则a的值为-2.