题目内容
已知:如图在△ABC中,BD,CE为两条高线,F为BD上一点,G为CE延长线上一点,BF=AC,CG=AB.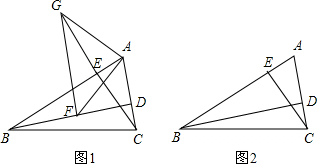
(1)请你判断△AFG的形状并证明.
(2)当F为BD反向延长线上一点,G为CE反向延线上一点,其它条件不变,(1)中的结论是否仍然成立?请你画出图形,并证明你的结论.

(1)请你判断△AFG的形状并证明.
(2)当F为BD反向延长线上一点,G为CE反向延线上一点,其它条件不变,(1)中的结论是否仍然成立?请你画出图形,并证明你的结论.
考点:全等三角形的判定与性质
专题:
分析:(1)先证∠ABF=∠ACE,再证明△ABF≌△GCA(SAS),得出AF=AG,∠BAF=∠CGA,然后证出∠FAG=90°即可;
(2)先证∠ABF=∠GCA,再证明△ABF≌△GCA(SAS),可得AF=AG,∠BAF=∠CGA,再由角的关系证出∠FAG=90°即可证出△AFG是等腰直角三角形.
(2)先证∠ABF=∠GCA,再证明△ABF≌△GCA(SAS),可得AF=AG,∠BAF=∠CGA,再由角的关系证出∠FAG=90°即可证出△AFG是等腰直角三角形.
解答:解:(1)△AFG为等腰直角三角形;
证明:∵BD、CE是△ABC的高,
∴∠ADB=∠AEC=90°,
∴∠ABF+∠BAD=90°,∠ACE+∠BAD=90°,
∴∠ABF=∠ACE,
在△ABF和△GCA中,
∴△ABF≌△GCA(SAS),
∴AF=AG,∠BAF=∠CGA,
∵∠CGA+∠GAE=90°,
∴∠BAF+∠GAE=90°,
即∠FAG=90°,
∴△AFG是等腰直角三角形;
(2)(1)中的结论成立;
证明:如图2所示:
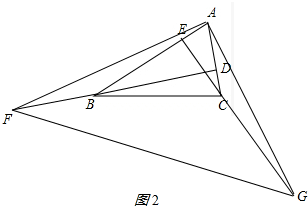 由(1)得,∠ABF=∠ACE,
由(1)得,∠ABF=∠ACE,
∴∠ABF=∠GCA,
在△ABF和△GCA中,
∴△ABF≌△GCA(SAS),
∴AF=AG,∠BAF=∠CGA,
∵∠ACE=∠CGA+∠CAG,∠ACE+∠EAC=90°,
∴∠BAF+∠CAG+∠EAC=90°,
即∠FAG=90°,
∴△AFG是等腰直角三角形.
证明:∵BD、CE是△ABC的高,
∴∠ADB=∠AEC=90°,
∴∠ABF+∠BAD=90°,∠ACE+∠BAD=90°,
∴∠ABF=∠ACE,
在△ABF和△GCA中,
|
∴△ABF≌△GCA(SAS),
∴AF=AG,∠BAF=∠CGA,
∵∠CGA+∠GAE=90°,
∴∠BAF+∠GAE=90°,
即∠FAG=90°,
∴△AFG是等腰直角三角形;
(2)(1)中的结论成立;
证明:如图2所示:
 由(1)得,∠ABF=∠ACE,
由(1)得,∠ABF=∠ACE,∴∠ABF=∠GCA,
在△ABF和△GCA中,
|
∴△ABF≌△GCA(SAS),
∴AF=AG,∠BAF=∠CGA,
∵∠ACE=∠CGA+∠CAG,∠ACE+∠EAC=90°,
∴∠BAF+∠CAG+∠EAC=90°,
即∠FAG=90°,
∴△AFG是等腰直角三角形.
点评:本题考查了全等三角形的判定与性质以及等腰直角三角形的判定;证明角相等和三角形全等是解决问题的关键.

练习册系列答案
相关题目
 如图,AB是半圆O的直径,D,E是半圆上任意两点,连结AD,DE,AE与BD相交于点C,要使△ADC与△ABD相似,可以添加一个条件.下列添加的条件其中错误的是( )
如图,AB是半圆O的直径,D,E是半圆上任意两点,连结AD,DE,AE与BD相交于点C,要使△ADC与△ABD相似,可以添加一个条件.下列添加的条件其中错误的是( )| A、∠ACD=∠DAB |
| B、AD=DE |
| C、AD2=BD•CD |
| D、AD•AB=AC•BD |
 如图,一扇形纸扇完全打开后,外侧两竹条AB、AC的夹角为120°,AB长为30cm,贴纸部分BD长为20cm,贴纸部分的面积为( )cm2.
如图,一扇形纸扇完全打开后,外侧两竹条AB、AC的夹角为120°,AB长为30cm,贴纸部分BD长为20cm,贴纸部分的面积为( )cm2.A、
| ||
B、
| ||
| C、800π | ||
| D、500π |
 先作图,再证明.
先作图,再证明. 如图,△ABD中,AB=AD,AC平分∠BAD,交BD于点E.
如图,△ABD中,AB=AD,AC平分∠BAD,交BD于点E. 如图,已知∠BOC=2∠AOC,OD平分∠AOB,且∠COD=19°,求∠AOB的度数.
如图,已知∠BOC=2∠AOC,OD平分∠AOB,且∠COD=19°,求∠AOB的度数. 如图已知直线y=
如图已知直线y=