题目内容
 先作图,再证明.
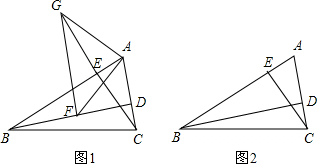
先作图,再证明.(1)在所给出的图形中完成一下作图(保留作图痕迹):
①作∠ACB的平分线CD,交AB于D;
②延长BC到E,使CE=CA,连接AE.
(2)求证:CD∥AE.
考点:作图—复杂作图
专题:
分析:(1)利用直尺和圆规即可作出;
(2)根据等腰对等角以及三角形的外角的性质即可证得∠ACD=∠CEA,进而证明.
(2)根据等腰对等角以及三角形的外角的性质即可证得∠ACD=∠CEA,进而证明.
解答:(1)解:如图所示:
 ;
;
(2)证明:∵CE=CA,
∴∠CAE=∠AEC,
又∵∠ACB=∠CAE+∠AEC,
∠ACD=
∠ACB,
∴∠ACD=∠CEA,
∴CD∥AE.
 ;
;(2)证明:∵CE=CA,
∴∠CAE=∠AEC,
又∵∠ACB=∠CAE+∠AEC,
∠ACD=
| 1 |
| 2 |
∴∠ACD=∠CEA,
∴CD∥AE.
点评:本题考查了尺规作图和等腰三角形的性质:等边对等角,正确理解性质定理是关键.

练习册系列答案
 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案
相关题目
| 3x-6 |
| A、x≥-1 | B、x≠-2 |
| C、x≥2 | D、x≠2 |
用配方法解一元二次方程x2+4x-5=0,此方程可变形为( )
| A、(x-2)2=9 |
| B、(x+2)2=9 |
| C、(x+2)2=1 |
| D、(x-2)2=1 |
 如图,Rt△ABC中,∠C=90°,AC=3,以AD为直径的半圆的面积为
如图,Rt△ABC中,∠C=90°,AC=3,以AD为直径的半圆的面积为| 25π |
| 8 |
| A、2 | B、4 | C、5 | D、2π |
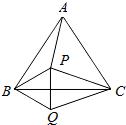 如图所示,点P是等边三角形ABC内的一点,连接PA、PB、PC以BP为边作∠PBQ=60°,且BQ=BP,连接CQ.
如图所示,点P是等边三角形ABC内的一点,连接PA、PB、PC以BP为边作∠PBQ=60°,且BQ=BP,连接CQ. E为正方形ABCD的边BC上一点,BE=3cm,EC=1cm,DF⊥AE交AE于点F,求DF的长.
E为正方形ABCD的边BC上一点,BE=3cm,EC=1cm,DF⊥AE交AE于点F,求DF的长.