题目内容
 如图,△ABD中,AB=AD,AC平分∠BAD,交BD于点E.
如图,△ABD中,AB=AD,AC平分∠BAD,交BD于点E.(1)求证:△BCD是等腰三角形;
(2)若∠ABD=50°,∠BCD=130°,求∠ABC的度数.
考点:等腰三角形的判定与性质
专题:
分析:(1)证明△ABC≌△ADC,即可得出BC=DC;
(2)在等腰三角形BCD中先求出∠CBD=∠CDB=25°,即可求出∠ABC=∠ABD+∠CBD=75°.
(2)在等腰三角形BCD中先求出∠CBD=∠CDB=25°,即可求出∠ABC=∠ABD+∠CBD=75°.
解答:解:(1)证明:∵AC平分∠BAD,
∴∠BAC=∠DAC,
在△ABC和△ADC中,
∴△ABC≌△ADC(SAS),
∴BC=DC,
∴△BCD是等腰三角形;
(2)∵BC=DC,∠BCD=130°,
∴∠CBD=∠CDB=
(180°-∠BCD)=
(180°-130°)=25°,
∴∠ABC=∠ABD+∠CBD=50°+25°=75°.
∴∠BAC=∠DAC,
在△ABC和△ADC中,
|
∴△ABC≌△ADC(SAS),
∴BC=DC,
∴△BCD是等腰三角形;
(2)∵BC=DC,∠BCD=130°,
∴∠CBD=∠CDB=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠ABC=∠ABD+∠CBD=50°+25°=75°.
点评:本题考查了全等三角形的判定与性质和等腰三角形的判定与性质;证明三角形全等证出等腰三角形是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
用配方法解一元二次方程x2+4x-5=0,此方程可变形为( )
| A、(x-2)2=9 |
| B、(x+2)2=9 |
| C、(x+2)2=1 |
| D、(x-2)2=1 |
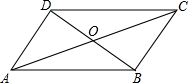 如图所示,在?ABCD中,AD⊥BD,AD=4,OD=3.
如图所示,在?ABCD中,AD⊥BD,AD=4,OD=3.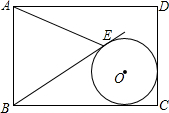 如图,在矩形ABCD中,AB=3,AD=4,⊙O与边BC,CD相切,现有一条过点B的直线与⊙O相切于点E,连接BE,△ABE恰为等边三角形,则⊙O的半径为
如图,在矩形ABCD中,AB=3,AD=4,⊙O与边BC,CD相切,现有一条过点B的直线与⊙O相切于点E,连接BE,△ABE恰为等边三角形,则⊙O的半径为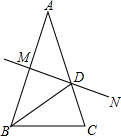 如图,已知AB=AC,∠A=36°,AB的中垂线MN交AC于点D,交AB于点M,
如图,已知AB=AC,∠A=36°,AB的中垂线MN交AC于点D,交AB于点M,
 如图所示,在平面直角坐标系xOy中,已知P,Q两点的纵坐标分别为6,2,直线PQ与x轴所成锐角为30°.
如图所示,在平面直角坐标系xOy中,已知P,Q两点的纵坐标分别为6,2,直线PQ与x轴所成锐角为30°. 如图,AB∥CD∥EF,EC平分∠AEF,∠3=140°,则∠1=
如图,AB∥CD∥EF,EC平分∠AEF,∠3=140°,则∠1= 如图,在锐角三角形ABC中,CM为AB边上的高,P为BC的中点,连接MP,在AC上找到一点N,使NP=MP,连接BN,试判断BN与AC的位置关系,并说明理由.
如图,在锐角三角形ABC中,CM为AB边上的高,P为BC的中点,连接MP,在AC上找到一点N,使NP=MP,连接BN,试判断BN与AC的位置关系,并说明理由.