题目内容
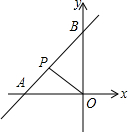 如图已知直线y=
如图已知直线y=| 3 |
| 4 |
(1)若△AOP的面积为2,求点P的坐标;
(2)设P的横坐标为x,△AOP的面积为S,写出S与x之间的函数关系式.
考点:一次函数图象上点的坐标特征
专题:
分析:(1)先求出点A的坐标,再根据三角形的面积公式即可得出结论;
(2)先根据点P在线段上得出P点纵坐标,再根据三角形的面积公式即可得出结论.
(2)先根据点P在线段上得出P点纵坐标,再根据三角形的面积公式即可得出结论.
解答:解:(1)设P点纵坐标为h,
∵当y=0时,x=-4,
∴A(-4,0),即OA=4.
∵△AOP的面积为2,即
OA•h=2,解得h=1,
∵点P是线段AB上的动点,
∴当y=1时,x=-
,即P(-
,1);
(2)∵点P是线段AB上的动点,P的横坐标为x,
∴P点的纵坐标为y=
x+3,.
∵△AOP的面积为S,
∴
OA•(
x+3)=S,即2(
x+3)=S,故S=
x+6.
∵当y=0时,x=-4,
∴A(-4,0),即OA=4.
∵△AOP的面积为2,即
| 1 |
| 2 |
∵点P是线段AB上的动点,
∴当y=1时,x=-
| 8 |
| 3 |
| 8 |
| 3 |
(2)∵点P是线段AB上的动点,P的横坐标为x,
∴P点的纵坐标为y=
| 3 |
| 4 |
∵△AOP的面积为S,
∴
| 1 |
| 2 |
| 3 |
| 4 |
| 3 |
| 4 |
| 3 |
| 2 |
点评:本题考查的是一次函数图象上点的坐标特点,熟知一次函数图象上各点的坐标一定适合此函数的解析式是解答此题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 如图,a,b,c为实数,则|a-c|-
如图,a,b,c为实数,则|a-c|-| (b-a)2 |
| A、-2b | B、-2c |
| C、-2a+2b | D、0 |
 E为正方形ABCD的边BC上一点,BE=3cm,EC=1cm,DF⊥AE交AE于点F,求DF的长.
E为正方形ABCD的边BC上一点,BE=3cm,EC=1cm,DF⊥AE交AE于点F,求DF的长.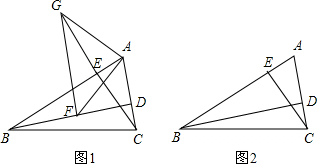
 当∠1,∠2,∠3满足条件
当∠1,∠2,∠3满足条件 如图,AB∥CD∥EF,EC平分∠AEF,∠3=140°,则∠1=
如图,AB∥CD∥EF,EC平分∠AEF,∠3=140°,则∠1= 如图,在长方体ABCD-A′B′C′D′中,与棱AB平行的有
如图,在长方体ABCD-A′B′C′D′中,与棱AB平行的有