题目内容
 如图,AB是半圆O的直径,D,E是半圆上任意两点,连结AD,DE,AE与BD相交于点C,要使△ADC与△ABD相似,可以添加一个条件.下列添加的条件其中错误的是( )
如图,AB是半圆O的直径,D,E是半圆上任意两点,连结AD,DE,AE与BD相交于点C,要使△ADC与△ABD相似,可以添加一个条件.下列添加的条件其中错误的是( )| A、∠ACD=∠DAB |
| B、AD=DE |
| C、AD2=BD•CD |
| D、AD•AB=AC•BD |
考点:相似三角形的判定,圆周角定理
专题:
分析:如图,将所给的四个条件逐一判断、分析,即可解决问题.
解答: 解:如图,若AD•AB=AC•BD,
解:如图,若AD•AB=AC•BD,
则
=
,而∠DAC=∠DBA不一定成立,
∴△ADC与△ABD不一定相似,
故选D.
 解:如图,若AD•AB=AC•BD,
解:如图,若AD•AB=AC•BD,则
| AD |
| BD |
| AC |
| AB |
∴△ADC与△ABD不一定相似,
故选D.
点评:该题是一道条件探究型命题,主要考查了相似三角形的判定问题;解题的关键是牢固掌握相似三角形每个判定方法,灵活分析、判断、运用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
| 3x-6 |
| A、x≥-1 | B、x≠-2 |
| C、x≥2 | D、x≠2 |
 如图,a,b,c为实数,则|a-c|-
如图,a,b,c为实数,则|a-c|-| (b-a)2 |
| A、-2b | B、-2c |
| C、-2a+2b | D、0 |
 E为正方形ABCD的边BC上一点,BE=3cm,EC=1cm,DF⊥AE交AE于点F,求DF的长.
E为正方形ABCD的边BC上一点,BE=3cm,EC=1cm,DF⊥AE交AE于点F,求DF的长. 如图,一菱形ABCD的边长为2,且∠ABC=120°,点E是BC的中点,点P为BD上一点,且△PCE的周长最小.
如图,一菱形ABCD的边长为2,且∠ABC=120°,点E是BC的中点,点P为BD上一点,且△PCE的周长最小. 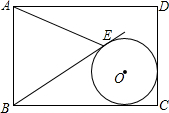 如图,在矩形ABCD中,AB=3,AD=4,⊙O与边BC,CD相切,现有一条过点B的直线与⊙O相切于点E,连接BE,△ABE恰为等边三角形,则⊙O的半径为
如图,在矩形ABCD中,AB=3,AD=4,⊙O与边BC,CD相切,现有一条过点B的直线与⊙O相切于点E,连接BE,△ABE恰为等边三角形,则⊙O的半径为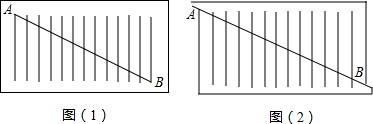
 当∠1,∠2,∠3满足条件
当∠1,∠2,∠3满足条件