题目内容
12.在△ABC中,∠C=90°,AC=3cm,BC=4cm.(1)求这个三角形的斜边AB的长和斜边上的高CD的长;
(2)求斜边被分成的两部分AD和BD的长.
分析 (1)由勾股定理求出AB,由三角形的面积的计算方法即可求出斜边上的高CD的长;
(2)由勾股定理求出AD,即可得出BD的长.
解答  解:(1)如图所示:∵∠ACB=90°,
解:(1)如图所示:∵∠ACB=90°,
∴AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=$\sqrt{{3}^{2}+{4}^{2}}$=5(cm);
∵△ABC的面积=$\frac{1}{2}$AB•CD=$\frac{1}{2}$AC•BC,
∴CD=$\frac{AC•BC}{AB}$=$\frac{3×4}{5}$=2.4(cm);
(2)∵CD是斜边AB上的高,
∴CD⊥AB,
∴∠ADC=90°,
∴AD=$\sqrt{A{C}^{2}-C{D}^{2}}$=$\sqrt{{3}^{2}-2.{4}^{2}}$=1.8(cm),
∴BD=AB-AD=3.2(cm).
点评 本题考查了勾股定理、直角三角形面积的计算方法;熟练掌握勾股定理,并能进行推理计算是解决问题的关键.

练习册系列答案
相关题目
 如图,在等边三角形ABC中,P是△ABC的一点,PA=1,PB=$\sqrt{7}$,PC=2$\sqrt{2}$,求∠APB的大小.
如图,在等边三角形ABC中,P是△ABC的一点,PA=1,PB=$\sqrt{7}$,PC=2$\sqrt{2}$,求∠APB的大小.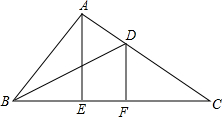 在△ABC中,AE⊥BC于点E,∠BAE:∠CAE=4:7,BD平分∠ABC,点F在BC上,∠CDF=70°,∠ABD=25°.
在△ABC中,AE⊥BC于点E,∠BAE:∠CAE=4:7,BD平分∠ABC,点F在BC上,∠CDF=70°,∠ABD=25°. 已知:如图,在平面直角坐标系中.
已知:如图,在平面直角坐标系中.
 (1)如图1,等边三角形ABC的边长为6,建立适当的直角坐标系,并写出各点的坐标.
(1)如图1,等边三角形ABC的边长为6,建立适当的直角坐标系,并写出各点的坐标. 如图,设⊙O是边长为2的正方形的内切圆,⊙O1与⊙O外切且与正方形的边长BC,CD相切,求⊙O1的面积.
如图,设⊙O是边长为2的正方形的内切圆,⊙O1与⊙O外切且与正方形的边长BC,CD相切,求⊙O1的面积.