Question

2．如图，在等边三角形ABC中，P是△ABC的一点，PA=1，PB=$\sqrt{7}$，PC=2$\sqrt{2}$，求∠APB的大小．

Answer 1

分析 将△BCP绕B逆时针旋转60°，点C和A重合，P到P′，连接PP′，得出等边三角形PBP′，求出∠BPP′=60°，推出直角三角形APP′，求出∠APP′，即可求出答案．

解答 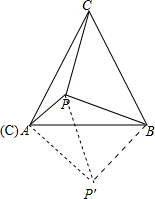解：将△BCP绕B逆时针旋转60°，点C和A重合，P到P′，连接PP′，
∵∠PBP′=60°，BP=BP′，
∴△PBP′是等边三角形，
∴∠BPP′=60°，
∴PP′=PB=$\sqrt{7}$，AP′=PC=2$\sqrt{2}$，PA=1，
∵PP′²+PA²=AP′²，
∴∠APP′=90°，
∴∠APB=60°+90°=150°．

点评 本题考查了等边本题考查了旋转的性质，勾股定理的逆定理，解此题的关键是正确作辅助线，把PA、PB、PC放在“一个三角形”中，主要考查学生的思维能力和运用性质进行推理的能力．