题目内容
4.已知⊙O和⊙O上的一点A,茗茗向以点A为顶点,在⊙O中作内接正多边形,以下是她的作法:①连接AO并延长交⊙O于点B;②以点A为圆心,AO长为半径画弧,交⊙O于点C,D,③以点B为圆心,BO长为半径画弧,交⊙O于点E,F;④顺次连接⊙O上的各点,连接所得的多边形即为茗茗所要作的正多边形,则此正多边形为正六边形.分析 连接OC、OD、OE、OF,由作图得出AC=AD=AO=BO=BE=BF=OC=OD=OE=OF,得出△OAC是等边三角形,因此∠OAC=∠AOC=60°,同理:∠OAD=60°,∠BOE=60°,证出:∠CAD=∠ADF=∠DFB=∠FBE=∠BEC=∠ACE=120°,AD=CE=BE=BF=DF=AD,即可得出六边形ACEBFD为正六边形.
解答 解:如图所示: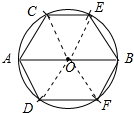
六边形ACEBFD为正六边形;理由如下:
连接OC、OD、OE、OF,
根据题意得:AC=AD=AO=BO=BE=BF=OC=OD=OE=OF,
∴△OAC是等边三角形,
∴∠OAC=∠AOC=60°,
同理:∠OAD=60°,∠BOE=60°,
∴△COE是等边三角形CE=OC=AC,∠CAD=120°,
同理:∠ADF=∠DFB=∠FBE=∠BEC=∠ACE=120°,
又∵AD=CE=BE=BF=DF=AD,
∴六边形ACEBFD为正六边形;
故答案为:正六边形.
点评 本题考查了正六边形的判定、作图、等边三角形的判定与性质;熟练掌握等边三角形的判定与性质,证出多边形的各角相等、各边相等是解决问题的关键.

练习册系列答案
相关题目
19.有五张彩纸(形状、大小、质地都相同),茗茗在上面分别写下了5个不同的字母,分别是B,N,S,T,O,将彩纸背面朝上洗匀,从中抽取一张彩纸,正面的字母一定满足既是轴对称图形,又是中心对称图形的概率是( )
| A. | $\frac{1}{5}$ | B. | $\frac{2}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
13.已知$\sqrt{{(1-2x)}^2}=2x-1$,则x的取值范围是( )
| A. | x≥$\frac{1}{2}$ | B. | x≤$\frac{1}{2}$ | C. | x>$\frac{1}{2}$ | D. | x<$\frac{1}{2}$ |
14.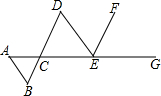 如图,已知BD∥EF,EF平分∠DEG,∠A=∠AED,则与∠B相等的角有( )
如图,已知BD∥EF,EF平分∠DEG,∠A=∠AED,则与∠B相等的角有( )
 如图,已知BD∥EF,EF平分∠DEG,∠A=∠AED,则与∠B相等的角有( )
如图,已知BD∥EF,EF平分∠DEG,∠A=∠AED,则与∠B相等的角有( )| A. | 0个 | B. | 1个 | C. | 3个 | D. | 5个 |
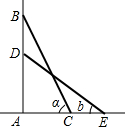 如图,一架梯子斜靠在墙上,梯子与地面的夹角为a(a=∠BCA),当梯顶下滑1m时,这架梯子与地面的夹角为b(b=∠DEA,A、C、E三点在一条直线上),求梯子的长.
如图,一架梯子斜靠在墙上,梯子与地面的夹角为a(a=∠BCA),当梯顶下滑1m时,这架梯子与地面的夹角为b(b=∠DEA,A、C、E三点在一条直线上),求梯子的长.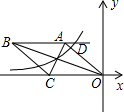 如图,在平面直角坐标系中,菱形OABC的一边在x轴上,反比例函数y-$\frac{k}{x}$(k≠0)的图象经过菱形两对交线的交点,且与AB所在直线交于点D,已知AC•OB=64$\sqrt{2}$,OC=8,则以下结论:①k=-16$\sqrt{2}$;②点D的纵坐标为4$\sqrt{2}$;③∠OBC=22.5°;④反比例函数y=-$\frac{k}{x}$随x的增大而增大;⑤tan∠AOC=1,其中正确的是( )
如图,在平面直角坐标系中,菱形OABC的一边在x轴上,反比例函数y-$\frac{k}{x}$(k≠0)的图象经过菱形两对交线的交点,且与AB所在直线交于点D,已知AC•OB=64$\sqrt{2}$,OC=8,则以下结论:①k=-16$\sqrt{2}$;②点D的纵坐标为4$\sqrt{2}$;③∠OBC=22.5°;④反比例函数y=-$\frac{k}{x}$随x的增大而增大;⑤tan∠AOC=1,其中正确的是( )