题目内容
14．两条直线相交所成的四个角都相等时，这两条直线的位置关系是（ ）| A． | 平行 | B． | 相交 | C． | 垂直 | D． | 不能确定 |
分析 两条直线相交所成的四个角都相等时，根据这四个角的和为360°，得出这四个角都是90°，由垂直的定义即可得出这两条直线互相垂直．
解答 解：两条直线相交所成的四个角都相等时，则每一个角都为90°，所以这两条直线垂直．
故选C．
点评 本题考查了垂直的定义，解题的关键是知道两直线相交所成的四个角中，若有一个角为直角，则这两条直线互相垂直．
练习册系列答案
相关题目
2．下列说法正确的个数是（ ）
①-4没有立方根；②-5的立方根是-$\root{3}{-5}$；③1的立方根是±1；④$\frac{1}{36}$的立方根是$\frac{1}{6}$；⑤64的立方根是4．
①-4没有立方根；②-5的立方根是-$\root{3}{-5}$；③1的立方根是±1；④$\frac{1}{36}$的立方根是$\frac{1}{6}$；⑤64的立方根是4．
| A． | 1个 | B． | 2个 | C． | 3个 | D． | 4个 |
5．
如图，在方格纸上，△ABC经过变换得到△DEF，下列对变换过程的叙述正确的是（ ）
如图，在方格纸上，△ABC经过变换得到△DEF，下列对变换过程的叙述正确的是（ ）| A． | △ABC绕着点A顺时针旋转90°，再向右平移7格 | |
| B． | △ABC向右平移4格，再向上平移7格 | |
| C． | △ABC绕着点A逆时针旋转90°，再向右平移7格 | |
| D． | △ABC向右平移4格，再绕着点B逆时针旋转90° |
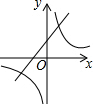
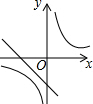
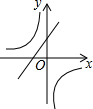
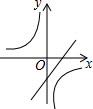
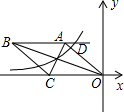如图，在平面直角坐标系中，菱形OABC的一边在x轴上，反比例函数y-$\frac{k}{x}$（k≠0）的图象经过菱形两对交线的交点，且与AB所在直线交于点D，已知AC•OB=64$\sqrt{2}$，OC=8，则以下结论：①k=-16$\sqrt{2}$；②点D的纵坐标为4$\sqrt{2}$；③∠OBC=22.5°；④反比例函数y=-$\frac{k}{x}$随x的增大而增大；⑤tan∠AOC=1，其中正确的是（ ）
19．化简$\frac{1}{3-2\sqrt{2}}$结果正确的是（ ）
| A． | 3$+2\sqrt{2}$ | B． | 3$-\sqrt{2}$ | C． | 17$+12\sqrt{2}$ | D． | 17-12$\sqrt{2}$ |
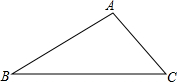已知：在△ABC中，∠B=45°，∠C=30°，AC=2．求：
如图，直线AB，CD相交于点O，OE⊥AB，垂足为O，∠BOD=20°，求∠COE的度数．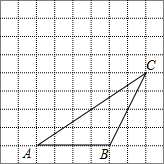
如下图，△ABC的顶点都在方格纸的格点上．将△ABC向左平移2格，再向上平移4格．请在图中画出平移后的三角形A′B′C′，再在图中画出三角形A′B′C′的高C′D′、中线A′E．