题目内容
18．先化简，再求值：（$\frac{1}{a-1}$-$\frac{1}{a+1}$）•$\frac{{a}^{2}-1}{a}$，从$\sqrt{2}$、1、0中选一个值作为a的值．分析 先根据分式混合运算的法则把原式进行化简，再选出合适的a的值代入进行计算即可．
解答 解：原式=$\frac{a+1-a+1}{（a-1）（a+1）}$•$\frac{（a-1）（a+1）}{a}$
=$\frac{2}{（a-1）（a+1）}$•$\frac{（a-1）（a+1）}{a}$
=$\frac{2}{a}$，
当a=$\sqrt{2}$时，原式=$\frac{2}{\sqrt{2}}$=$\sqrt{2}$．
点评 本题考查的是分式的化简求值，熟知分式混合运算的法则是解答此题的关键
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
9．水果商贩小李去水果批发市场采购被誉为“果中之王”的泰顺猕猴桃，他了解到猕猴桃有精品盒与普通盒两种包装，精品盒的批发价格每盒60元，普通盒的批发价格每盒40元，现小李购得精品盒与普通盒共60盒，费用共为3100元．
（1）问小李分别购买精品盒与普通盒多少盒？
（2）小李经营着甲、乙两家店铺，每家店铺每天部能售出精品盒与普通盒共30盒，并且每售出一盒精品盒与普通盒，在甲店获利分别为30元和40元，在乙店获利分别为24元和35元．现在小李要将购进的60盒弥猴桃分配给每个店铺各30盒，设分配给甲店精品盒a盒，请你根据题意填写下表：
小李希望在甲店获利不少于1000元的前提下，使自己获取的总利润W最大，应该如何分配？最大的总利润是多少？
（1）问小李分别购买精品盒与普通盒多少盒？
（2）小李经营着甲、乙两家店铺，每家店铺每天部能售出精品盒与普通盒共30盒，并且每售出一盒精品盒与普通盒，在甲店获利分别为30元和40元，在乙店获利分别为24元和35元．现在小李要将购进的60盒弥猴桃分配给每个店铺各30盒，设分配给甲店精品盒a盒，请你根据题意填写下表：
| 精品盒数量（盒） | 普通盒数量（盒） | 合计（盒） | |
| 甲店 | a | 30-a | 30 |
| 乙店 | 35-a | a-5 | 30 |
5．
如图，在方格纸上，△ABC经过变换得到△DEF，下列对变换过程的叙述正确的是（ ）
如图，在方格纸上，△ABC经过变换得到△DEF，下列对变换过程的叙述正确的是（ ）| A． | △ABC绕着点A顺时针旋转90°，再向右平移7格 | |
| B． | △ABC向右平移4格，再向上平移7格 | |
| C． | △ABC绕着点A逆时针旋转90°，再向右平移7格 | |
| D． | △ABC向右平移4格，再绕着点B逆时针旋转90° |
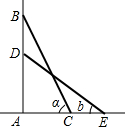如图，一架梯子斜靠在墙上，梯子与地面的夹角为a（a=∠BCA），当梯顶下滑1m时，这架梯子与地面的夹角为b（b=∠DEA，A、C、E三点在一条直线上），求梯子的长．
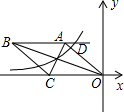如图，在平面直角坐标系中，菱形OABC的一边在x轴上，反比例函数y-$\frac{k}{x}$（k≠0）的图象经过菱形两对交线的交点，且与AB所在直线交于点D，已知AC•OB=64$\sqrt{2}$，OC=8，则以下结论：①k=-16$\sqrt{2}$；②点D的纵坐标为4$\sqrt{2}$；③∠OBC=22.5°；④反比例函数y=-$\frac{k}{x}$随x的增大而增大；⑤tan∠AOC=1，其中正确的是（ ）