题目内容
18．已知$x=2\sqrt{3}-\sqrt{5}$，求代数式$（17+4\sqrt{15}）x^2-（2\sqrt{3}+\sqrt{5}）x-2$的值．分析 将的值直接代入代数式，运用完全平方公式和平方差公式计算可得．
解答 解：当$x=2\sqrt{3}-\sqrt{5}$时，
原式=（17+4$\sqrt{15}$）（2$\sqrt{3}$-$\sqrt{5}$）2-（2$\sqrt{3}$+$\sqrt{5}$）（2$\sqrt{3}$-$\sqrt{5}$）-2
=（17+4$\sqrt{15}$）（17-4$\sqrt{15}$）-（12-5）-2
=172-（4$\sqrt{15}$）2-7-2
=289-240-9
=40．
点评 本题主要考查二次根式的化简求值，熟练掌握完全平方公式和平方差公式是解题的关键．
练习册系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
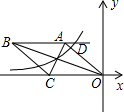如图，在平面直角坐标系中，菱形OABC的一边在x轴上，反比例函数y-$\frac{k}{x}$（k≠0）的图象经过菱形两对交线的交点，且与AB所在直线交于点D，已知AC•OB=64$\sqrt{2}$，OC=8，则以下结论：①k=-16$\sqrt{2}$；②点D的纵坐标为4$\sqrt{2}$；③∠OBC=22.5°；④反比例函数y=-$\frac{k}{x}$随x的增大而增大；⑤tan∠AOC=1，其中正确的是（ ）
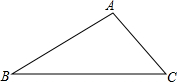已知：在△ABC中，∠B=45°，∠C=30°，AC=2．求：
13．已知$\sqrt{{（1-2x）}^2}=2x-1$，则x的取值范围是（ ）
| A． | x≥$\frac{1}{2}$ | B． | x≤$\frac{1}{2}$ | C． | x＞$\frac{1}{2}$ | D． | x＜$\frac{1}{2}$ |
如图，直线AB，CD相交于点O，OE⊥AB，垂足为O，∠BOD=20°，求∠COE的度数．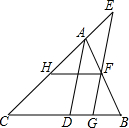
如图，已知∠ADB+∠EGC=180°，AD平分∠BAC，HF∥BC．