题目内容
20.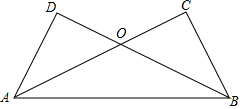 如图,AC⊥BC,AD⊥BD,AC与BD交于点O,AC=BD=8,AD=4.
如图,AC⊥BC,AD⊥BD,AC与BD交于点O,AC=BD=8,AD=4.(1)求证:OA=OB;
(2)求OA的长.
分析 (1)利用直角三角形全等的判定可证得Rt△ADB≌Rt△BCA,则可求得∠OAB=∠OBA,可证得OA=OB;
(2)在Rt△ADO中,设OA为x,利用勾股定理可求得OA的长.
解答 (1)证明:
∵AC⊥BC,AD⊥BD,
∴∠D=∠C=90°,
在Rt△ADB和Rt△BCA中
$\left\{\begin{array}{l}{BD=AC}\\{AB=BA}\end{array}\right.$,
∴Rt△ADB≌Rt△BCA(HL),
∴∠OAB=∠OBA,
∴OA=OB;
(2)解:
∵OA=OB,AC=BD=8,
∴OD=OC,
设OA为x,则OD=OC=8-x,
在Rt△ADO中,OA2=OD2+AD2,
∴x2=(8-x)2+42,解得x=5,
∴OA的长为5.
点评 本题主要考查全等三角形的判定和性质及勾股定理的应用,掌握直角三角形全等的判定方法HL是解题的关键.

练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案
相关题目
 如图,在四边形ABCD中,AD∥BC,BE平分∠ABC交边AD于点E,若∠ABC=50°,求∠AEB的度数.
如图,在四边形ABCD中,AD∥BC,BE平分∠ABC交边AD于点E,若∠ABC=50°,求∠AEB的度数.
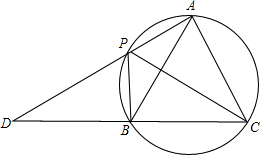 如图,四边形APBC是圆内接四边形,∠APB=120°,PC平分∠APB,AP,CB的延长线相交于点D.
如图,四边形APBC是圆内接四边形,∠APB=120°,PC平分∠APB,AP,CB的延长线相交于点D.