题目内容
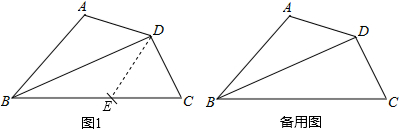
3．
如图，在四边形ABCD中，AD∥BC，BE平分∠ABC交边AD于点E，若∠ABC=50°，求∠AEB的度数．
分析 先根据角平分线的定义得到，∠ABC=2∠EBC，进而得出∠EBC=25°，再根据AD∥BC，即可得出∠AEB=∠EBC．
解答 解：∵BE平分∠ABC，
∴∠ABC=2∠EBC，
∵∠ABC=50°，
∴∠EBC=25°，
∵AD∥BC，
∴∠AEB=∠EBC，
∴∠AEB═25°．
点评 此题考查了平行四边形的性质与角平分线的定义的运用，解题时注意：两直线平行，内错角相等．
练习册系列答案
全优考典单元检测卷及归类总复习系列答案
相关题目
如图，已知直线y=$\frac{1}{2}$x与双曲线y=$\frac{k}{x}$（k＞0）相交于A、B两点，且点A的横坐标为4．
在一节数学课上，老师布置了一个任务：
8．抛物线y1=x2-2x+3与y轴交于A点，顶点是P，作PB⊥x轴于B点，若抛物线y2的形状和开口方向都与y1相同，并且经过A，B两点，则y2的顶点横坐标与纵坐标的符号分别是（ ）
| A． | 正，正 | B． | 负，正 | C． | 负，负 | D． | 正，负 |
15．
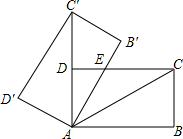如图，将矩形ABCD绕点A旋转至矩形A′B′C′D′的位置，此时AC的中点恰好与D点重合，AB′交CD于点E．若AB=3，则△AEC的面积为（ ）
如图，将矩形ABCD绕点A旋转至矩形A′B′C′D′的位置，此时AC的中点恰好与D点重合，AB′交CD于点E．若AB=3，则△AEC的面积为（ ）| A． | 3 | B． | 1.5 | C． | $2\sqrt{3}$ | D． | $\sqrt{3}$ |
12．已知一次函数y=kx+b与直线y=3x-2平行，与直线y=2x+3相交于y轴上一点，则k、b的值分别为（ ）
| A． | k=3，b=2 | B． | k=3，b=3 | C． | k=-2，b=3 | D． | k=2，b=3 |
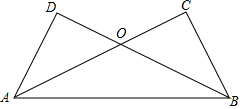如图，AC⊥BC，AD⊥BD，AC与BD交于点O，AC=BD=8，AD=4．