题目内容
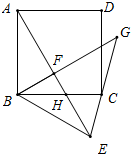 已知:正方形ABCD中,点F为正方形内一点(AF>BF),AF⊥BF,把△AFB沿BF所在的直线翻折,使点A落在点E处,AE交BC于点H,连接CE.
已知:正方形ABCD中,点F为正方形内一点(AF>BF),AF⊥BF,把△AFB沿BF所在的直线翻折,使点A落在点E处,AE交BC于点H,连接CE.(1)求∠HEC的度数;
(2)若直线EC、BF交于点G,判断线段BF与CG的数量关系并证明.
考点:正方形的性质,翻折变换(折叠问题)
专题:常规题型
分析:(1)根据AB=BC=BE可以判定A、C、E共圆,圆心为B,所以HEC为45°;
(2)易证RT△ABF∽RT△ACG,即可求得
=
,即可解题.
(2)易证RT△ABF∽RT△ACG,即可求得
| BF |
| CG |
| AB |
| AC |
解答:解:(1)连接AC,
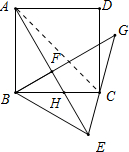
∵BE为AB翻转得到,
∴AB=BE,
∵AB=BC,
∴A、C、E三点共圆,且圆心为B.
∵AC弧所对的圆心角为90°,
∴AC弧对应圆周角∠HEC为45°;
(2)如图,
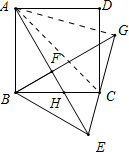
∵∠HEC=45°,
∴△AGE为等腰直角三角形,
∴∠GAF=45°,
∴△AFG为等腰直角三角形,
∴
=
=
,
∵∠BAC=∠GAF,
∴∠BAF=∠GAC,
∴RT△ABF∽RT△ACG
∴
=
=
,即CG=
BF.

∵BE为AB翻转得到,
∴AB=BE,
∵AB=BC,
∴A、C、E三点共圆,且圆心为B.
∵AC弧所对的圆心角为90°,
∴AC弧对应圆周角∠HEC为45°;
(2)如图,

∵∠HEC=45°,
∴△AGE为等腰直角三角形,
∴∠GAF=45°,
∴△AFG为等腰直角三角形,
∴
| AC |
| AB |
| AG |
| AF |
| 2 |
∵∠BAC=∠GAF,
∴∠BAF=∠GAC,
∴RT△ABF∽RT△ACG
∴
| BF |
| CG |
| AB |
| AC |
| ||
| 2 |
| 2 |
点评:本题考查了相似三角形的判定,考查了相似三角形对应边比例相等的性质,本题中求证RT△ABF∽RT△ACG是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
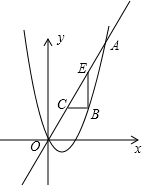 如图,已知抛物线y=
如图,已知抛物线y= 已知如图,在四边形ABCD中,∠A=90°,AB=3cm,BC=13cm,CD=12cm,AD=4cm,求四边形ABCD的面积.
已知如图,在四边形ABCD中,∠A=90°,AB=3cm,BC=13cm,CD=12cm,AD=4cm,求四边形ABCD的面积. 如图,四边形ABCD是一个长方形的台球桌,台球桌上还剩一个黑球没有被打进球袋,在点P的位置,现在轮到你打,你应该把在点Q位置的白球打到AB边上的哪一个点,才能反弹回来撞到黑球?试作图说明.
如图,四边形ABCD是一个长方形的台球桌,台球桌上还剩一个黑球没有被打进球袋,在点P的位置,现在轮到你打,你应该把在点Q位置的白球打到AB边上的哪一个点,才能反弹回来撞到黑球?试作图说明.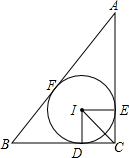 如图,在△ABC中,∠C=90°,内切圆⊙I与AC、BC分别相切于点E,D.
如图,在△ABC中,∠C=90°,内切圆⊙I与AC、BC分别相切于点E,D.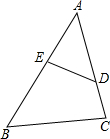 若∠ADE=∠B,AD=6,AB=12,DE=5,则BC的长为
若∠ADE=∠B,AD=6,AB=12,DE=5,则BC的长为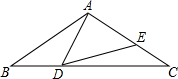 如图,△ABC中,AB=AC=2,∠B=40°.点D在线段BC上运动(点D不与B、C重合),连接AD,作∠ADE=40°,DE交线段AC于E.
如图,△ABC中,AB=AC=2,∠B=40°.点D在线段BC上运动(点D不与B、C重合),连接AD,作∠ADE=40°,DE交线段AC于E.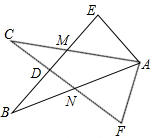 如图,在Rt△AEB和Rt△AFC中,BE与AC相交于点M,与CF相交于点D,AB与CF相交于N,∠E=∠F=90°,∠EAC=∠FAB,AE=AF.给出下列结论:①∠B=∠C;②CD=DN;③BE=CF;④△ACN≌△ABM.其中正确的结论是
如图,在Rt△AEB和Rt△AFC中,BE与AC相交于点M,与CF相交于点D,AB与CF相交于N,∠E=∠F=90°,∠EAC=∠FAB,AE=AF.给出下列结论:①∠B=∠C;②CD=DN;③BE=CF;④△ACN≌△ABM.其中正确的结论是