题目内容
 已知如图,在四边形ABCD中,∠A=90°,AB=3cm,BC=13cm,CD=12cm,AD=4cm,求四边形ABCD的面积.
已知如图,在四边形ABCD中,∠A=90°,AB=3cm,BC=13cm,CD=12cm,AD=4cm,求四边形ABCD的面积.考点:勾股定理,勾股定理的逆定理
专题:
分析:连接BD,先根据勾股定理求出BD的长度,再根据勾股定理的逆定理判断出△BCD的形状,最后利用三角形的面积公式求解即可.
解答:解:连接BD,如图所示:

∵∠A=90°,AB=3cm,AD=4cm,
∴BD=
=5cm,
在△ACD中,BD2+CD2=25+144=169=BC2,
∴△BCD是直角三角形,
∴S四边形ABCD=
AB•AD+
BD•CD=
×3×4+
×5×12=36(cm2).
故四边形ABCD的面积是36cm2.

∵∠A=90°,AB=3cm,AD=4cm,
∴BD=
| AB2+AD2 |
在△ACD中,BD2+CD2=25+144=169=BC2,
∴△BCD是直角三角形,
∴S四边形ABCD=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
故四边形ABCD的面积是36cm2.
点评:本题考查的是勾股定理、勾股定理的逆定理及三角形的面积,根据勾股定理的逆定理判断出△BCD的形状是解答此题的关键,难度适中.

练习册系列答案
相关题目
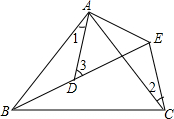 如图,AB=AC,AD=AE,∠BAC=∠DAE,B、D、E三点在同一条直线上且∠1=25°,∠2=30°,则∠3=
如图,AB=AC,AD=AE,∠BAC=∠DAE,B、D、E三点在同一条直线上且∠1=25°,∠2=30°,则∠3=
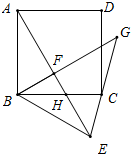 已知:正方形ABCD中,点F为正方形内一点(AF>BF),AF⊥BF,把△AFB沿BF所在的直线翻折,使点A落在点E处,AE交BC于点H,连接CE.
已知:正方形ABCD中,点F为正方形内一点(AF>BF),AF⊥BF,把△AFB沿BF所在的直线翻折,使点A落在点E处,AE交BC于点H,连接CE.