题目内容
若关于x的一元二次方程（m+1）x2-x+m2-1=0有一根为0，则m= ．
考点：一元二次方程的解
专题：
分析：把x=0代入已知方程列出关于m的新方程，通过解新方程来求m的值．
解答：解：∵关于x的一元二次方程（m+1）x2-x+m2-1=0有一根为0，
∴m2-1=0且m+1≠0，
∴（m+1）（m-1）=0且m+1≠0，
则m+1=0，
解得 m=-1．
故答案是：-1．
∴m2-1=0且m+1≠0，
∴（m+1）（m-1）=0且m+1≠0，
则m+1=0，
解得 m=-1．
故答案是：-1．
点评：本题考查了一元二次方程的解的定义．此题是根据一元二次方程的解的定义列出关于系数的方程，通过解方程来求系数的值．
练习册系列答案
相关题目
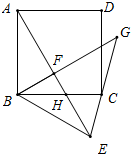已知：正方形ABCD中，点F为正方形内一点（AF＞BF），AF⊥BF，把△AFB沿BF所在的直线翻折，使点A落在点E处，AE交BC于点H，连接CE．
如图，已知正n边形边长为a，边心距为r，求正n边形的半径R、周长P和面积S．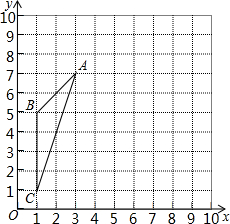
如图，在10×10的正方形网格中（每个小正方形的边长都为1个单位），△ABC的三个顶点都在格点上．建立如图所示的直角坐标系，
如图，AB=AD，∠BAD=∠CAE，AC=AE，求证：BC=DE．