题目内容
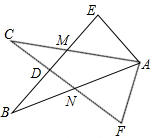 如图,在Rt△AEB和Rt△AFC中,BE与AC相交于点M,与CF相交于点D,AB与CF相交于N,∠E=∠F=90°,∠EAC=∠FAB,AE=AF.给出下列结论:①∠B=∠C;②CD=DN;③BE=CF;④△ACN≌△ABM.其中正确的结论是
如图,在Rt△AEB和Rt△AFC中,BE与AC相交于点M,与CF相交于点D,AB与CF相交于N,∠E=∠F=90°,∠EAC=∠FAB,AE=AF.给出下列结论:①∠B=∠C;②CD=DN;③BE=CF;④△ACN≌△ABM.其中正确的结论是考点:全等三角形的判定与性质
专题:
分析:根据题目中所给的大部分选项先判断该证明哪两个三角形全等,然后对各选项采取排除法得到正确选项.
解答:解:∵∠EAC=∠FAB,
∴∠EAB=∠CAF,
在△ABE和△ACF,
,
∴△ABE≌△ACF,
∴∠B=∠C,BE=CF.
由△AEB≌△AFC知:∠B=∠C,AC=AB;
在△ACN和△ABM,
,
∴△ACN≌△ABM;(故④正确)
由于条件不足,无法证得②CD=DN;
故答案为:①③④.
∴∠EAB=∠CAF,
在△ABE和△ACF,
|
∴△ABE≌△ACF,
∴∠B=∠C,BE=CF.
由△AEB≌△AFC知:∠B=∠C,AC=AB;
在△ACN和△ABM,
|
∴△ACN≌△ABM;(故④正确)
由于条件不足,无法证得②CD=DN;
故答案为:①③④.
点评:本题考查了全等三角形的判定和性质,判定两个三角形全等,先根据已知条件或求证的结论确定三角形,然后再根据三角形全等的判定方法,看缺什么条件,再去证什么条件.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
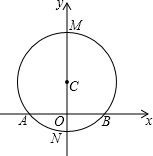 如图,AB是⊙C的弦,直径MN⊥AB于点O,MN=10,AB=8,以直线AB为x轴,直线MN为y轴建立坐标系.我们把横纵坐标都是整数的点叫做整数点,请写出⊙C上位于第二象限和第三象限的整数点的坐标
如图,AB是⊙C的弦,直径MN⊥AB于点O,MN=10,AB=8,以直线AB为x轴,直线MN为y轴建立坐标系.我们把横纵坐标都是整数的点叫做整数点,请写出⊙C上位于第二象限和第三象限的整数点的坐标已知(a+b)2=11,(a-b)2=7,则a2+b2等于( )
| A、4 | B、18 | C、9 | D、8 |
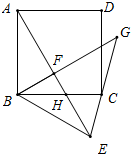 已知:正方形ABCD中,点F为正方形内一点(AF>BF),AF⊥BF,把△AFB沿BF所在的直线翻折,使点A落在点E处,AE交BC于点H,连接CE.
已知:正方形ABCD中,点F为正方形内一点(AF>BF),AF⊥BF,把△AFB沿BF所在的直线翻折,使点A落在点E处,AE交BC于点H,连接CE. 如图,AB=AD,∠BAD=∠CAE,AC=AE,求证:BC=DE.
如图,AB=AD,∠BAD=∠CAE,AC=AE,求证:BC=DE.