题目内容
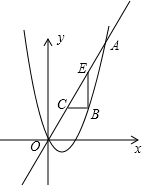 如图,已知抛物线y=
如图,已知抛物线y=| 1 |
| 2 |
(1)求抛物线的函数表达式;
(2)设点B的横坐标为m,当m取何值时,BE的长达到最大值,并求出该最大值;
(3)以BC,BE为边构造矩形BCDE,设点D的坐标为(m,n),求出m,n之间的关系式.
考点:二次函数综合题
专题:
分析:(1)将点A的坐标代入直线解析式求出a的值,继而将点A的坐标代入抛物线解析式可得出b的值,继而得出抛物线解析式;
(2)根据点B的横坐标为m,表示出点B的坐标是(m,
m2-m),点E的坐标为(m,2m),根据两点间的距离公式和配方法即可求解;
(3)根据点D的坐标,可得出点E的坐标,点C的坐标,继而确定点B的坐标,将点B的坐标代入抛物线解析式可求出m,n之间的关系式.
(2)根据点B的横坐标为m,表示出点B的坐标是(m,
| 1 |
| 2 |
(3)根据点D的坐标,可得出点E的坐标,点C的坐标,继而确定点B的坐标,将点B的坐标代入抛物线解析式可求出m,n之间的关系式.
解答:解:(1)∵点A(a,12)在直线y=2x上,
∴12=2a,
解得:a=6,
又∵点A是抛物线y=
x2+bx上的一点,
将点A(6,12)代入y=
x2+bx,可得b=-1,
∴抛物线解析式为y=
x2-x.
(2)∵点B的横坐标为m,
∴点B的坐标是(m,
m2-m),点E的坐标为(m,2m),
∴BE=2m-(
m2-m)=-
(m-3)2+
,
∴当m取3时,BE的长达到最大值,最大值是
;
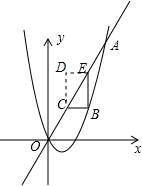
(3)∵直线OA的解析式为:y=2x,
点D的坐标为(m,n),
∴点E的坐标为(
n,n),点C的坐标为(m,2m),
∴点B的坐标为(
n,2m),
把点B(
n,2m)代入y=
x2-x,可得m=
n2-
n,
∴m、n之间的关系式为m=
n2-
n.
∴12=2a,
解得:a=6,
又∵点A是抛物线y=
| 1 |
| 2 |
将点A(6,12)代入y=
| 1 |
| 2 |
∴抛物线解析式为y=
| 1 |
| 2 |
(2)∵点B的横坐标为m,
∴点B的坐标是(m,
| 1 |
| 2 |
∴BE=2m-(
| 1 |
| 2 |
| 1 |
| 2 |
| 9 |
| 2 |
∴当m取3时,BE的长达到最大值,最大值是
| 9 |
| 2 |

(3)∵直线OA的解析式为:y=2x,
点D的坐标为(m,n),
∴点E的坐标为(
| 1 |
| 2 |
∴点B的坐标为(
| 1 |
| 2 |
把点B(
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 16 |
| 1 |
| 4 |
∴m、n之间的关系式为m=
| 1 |
| 16 |
| 1 |
| 4 |
点评:本题考查了二次函数的综合,涉及了两点间的距离公式、配方法、矩形的性质、待定系数法求二次函数解析式的知识,解答本题需要同学们能理解矩形四个顶点的坐标之间的关系.

练习册系列答案
 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案
相关题目
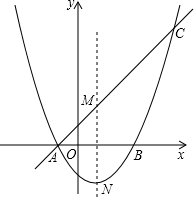 如图,抛物线y=
如图,抛物线y=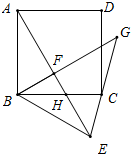 已知:正方形ABCD中,点F为正方形内一点(AF>BF),AF⊥BF,把△AFB沿BF所在的直线翻折,使点A落在点E处,AE交BC于点H,连接CE.
已知:正方形ABCD中,点F为正方形内一点(AF>BF),AF⊥BF,把△AFB沿BF所在的直线翻折,使点A落在点E处,AE交BC于点H,连接CE.