题目内容
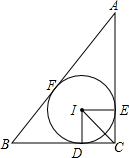 如图,在△ABC中,∠C=90°,内切圆⊙I与AC、BC分别相切于点E,D.
如图,在△ABC中,∠C=90°,内切圆⊙I与AC、BC分别相切于点E,D.(1)试判断四边形CDIE的形状,并说明理由;
(2)若此直角三角形的两条直角边的长分别为9和40,求线段CI的长.
考点:三角形的内切圆与内心
专题:计算题
分析:(1)根据内切圆的定义和切线的性质得∠IDC=∠IEC=90°,则易证得四边形CDIE为矩形,加上ID=IE,于是可判断四边形CDIE为正方形;
(2)先利用勾股定理计算出AB=41,如图,内切圆⊙I与AB切于F点,设⊙I的半径为r,则CD=CE=r,BD=9-r,AE=40-r,根据切线长定理得到BF=BD=9-r,AF=AE=40-r,则9-r+40-r=41,解方程求出r,然后根据正方形的性质计算CI.
(2)先利用勾股定理计算出AB=41,如图,内切圆⊙I与AB切于F点,设⊙I的半径为r,则CD=CE=r,BD=9-r,AE=40-r,根据切线长定理得到BF=BD=9-r,AF=AE=40-r,则9-r+40-r=41,解方程求出r,然后根据正方形的性质计算CI.
解答:解:(1)四边形CDIE为正方形.理由如下: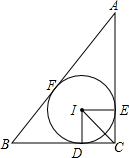
∵内切圆⊙I与AC、BC分别相切于点E,D,
∴ID⊥CB,IE⊥AC,
∴∠IDC=∠IEC=90°,
∵∠C=90°,
∴四边形CDIE为矩形,
∵ID=IE,
∴四边形CDIE为正方形;
(2)在Rt△ABC中,∵BC=9,AC=40,
∴AB=
=41,
如图,内切圆⊙I与AB切于F点,设⊙I的半径为r,则CD=CE=r,BD=9-r,AE=40-r,
∵D、E、F分别为切点,
∴BF=BD=9-r,AF=AE=40-r,
∵BF+AF=AB,
∴9-r+40-r=41,
∴r=4,
∴正方形CDIE的边长为4,
∴CI=4
.
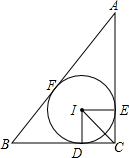
∵内切圆⊙I与AC、BC分别相切于点E,D,
∴ID⊥CB,IE⊥AC,
∴∠IDC=∠IEC=90°,
∵∠C=90°,
∴四边形CDIE为矩形,
∵ID=IE,
∴四边形CDIE为正方形;
(2)在Rt△ABC中,∵BC=9,AC=40,
∴AB=
| BC2+AC2 |
如图,内切圆⊙I与AB切于F点,设⊙I的半径为r,则CD=CE=r,BD=9-r,AE=40-r,
∵D、E、F分别为切点,
∴BF=BD=9-r,AF=AE=40-r,
∵BF+AF=AB,
∴9-r+40-r=41,
∴r=4,
∴正方形CDIE的边长为4,
∴CI=4
| 2 |
点评:本题考查了三角形的内切圆与内心:与三角形各边都相切的圆叫三角形的内切圆,三角形的内切圆的圆心叫做三角形的内心,这个三角形叫做圆的外切三角形.三角形的内心就是三角形三个内角角平分线的交点.也考查了切线的性质与切线长定理.

练习册系列答案
相关题目
已知(a+b)2=11,(a-b)2=7,则a2+b2等于( )
| A、4 | B、18 | C、9 | D、8 |
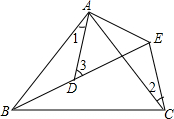 如图,AB=AC,AD=AE,∠BAC=∠DAE,B、D、E三点在同一条直线上且∠1=25°,∠2=30°,则∠3=
如图,AB=AC,AD=AE,∠BAC=∠DAE,B、D、E三点在同一条直线上且∠1=25°,∠2=30°,则∠3=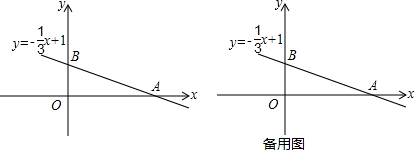
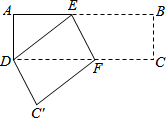 在长方形纸片ABCD中,AD=3cm,AB=9cm,按如图方式折叠,使点B与点D重合,折痕为EF,则DE=
在长方形纸片ABCD中,AD=3cm,AB=9cm,按如图方式折叠,使点B与点D重合,折痕为EF,则DE=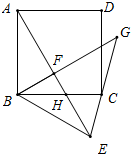 已知:正方形ABCD中,点F为正方形内一点(AF>BF),AF⊥BF,把△AFB沿BF所在的直线翻折,使点A落在点E处,AE交BC于点H,连接CE.
已知:正方形ABCD中,点F为正方形内一点(AF>BF),AF⊥BF,把△AFB沿BF所在的直线翻折,使点A落在点E处,AE交BC于点H,连接CE.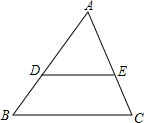 如图,已知DE∥BC,AD=5,DB=3,则S△ADE:S四边形DBCE=
如图,已知DE∥BC,AD=5,DB=3,则S△ADE:S四边形DBCE= 如图,已知正n边形边长为a,边心距为r,求正n边形的半径R、周长P和面积S.
如图,已知正n边形边长为a,边心距为r,求正n边形的半径R、周长P和面积S.