题目内容
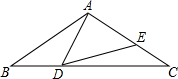 如图,△ABC中,AB=AC=2,∠B=40°.点D在线段BC上运动(点D不与B、C重合),连接AD,作∠ADE=40°,DE交线段AC于E.
如图,△ABC中,AB=AC=2,∠B=40°.点D在线段BC上运动(点D不与B、C重合),连接AD,作∠ADE=40°,DE交线段AC于E.(1)当∠BAD=20°时,∠EDC=
(2)当DC等于多少时△ABD≌△DCE?并说明理由;
(3)在点D的运动过程中,△ADE的形状也在改变,判断当∠BAD等于多少度时,△ADE是等腰三角形.
考点:全等三角形的判定与性质,等腰三角形的判定与性质
专题:动点型
分析:(1)根据外角等于不相邻两内角和可解题;
(2)当DC=AB=2时,即可求证△ABD≌△DCE;
(3)分类谈论,①若AD=AE时;②若DA=DE时,③若EA=ED时,即可解题.
(2)当DC=AB=2时,即可求证△ABD≌△DCE;
(3)分类谈论,①若AD=AE时;②若DA=DE时,③若EA=ED时,即可解题.
解答:解:(1)∵∠BAD=20°,∠B=40°,
∴∠ADC=60°,
∵∠ADE=40°,
∴∠EDC=20°.
(2)DC=AB=2时,
在△ABD和△DCE中,
,
∴△ABD≌△DCE(AAS);
(3)∵AB=AC,
∴∠B=∠C=40°,
①若AD=AE时,则∠ADE=∠AED=40°,
∵∠AED>∠C,
∴△ADE不可能是等腰三角形;
②若DA=DE时,即∠DAE=∠DEA=
(180°-40°)=70°,
∵∠BAC=180°-40°-40°=100°,
∴∠BAD=100°-70°=30°;
③若EA=ED时,∠ADE=∠DAE=40°,
∴∠BAD=100°-40°=60°,
∴当∠BAD=30°或60°时,△ADE是等腰三角形.
∴∠ADC=60°,
∵∠ADE=40°,
∴∠EDC=20°.
(2)DC=AB=2时,
在△ABD和△DCE中,
|
∴△ABD≌△DCE(AAS);
(3)∵AB=AC,
∴∠B=∠C=40°,
①若AD=AE时,则∠ADE=∠AED=40°,
∵∠AED>∠C,
∴△ADE不可能是等腰三角形;
②若DA=DE时,即∠DAE=∠DEA=
| 1 |
| 2 |
∵∠BAC=180°-40°-40°=100°,
∴∠BAD=100°-70°=30°;
③若EA=ED时,∠ADE=∠DAE=40°,
∴∠BAD=100°-40°=60°,
∴当∠BAD=30°或60°时,△ADE是等腰三角形.
点评:本题考查了全等三角形的判定,考查了等腰三角形的判定和腰长相等的性质.运用分类讨论解本题是解题的关键.

练习册系列答案
相关题目
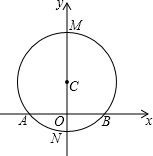 如图,AB是⊙C的弦,直径MN⊥AB于点O,MN=10,AB=8,以直线AB为x轴,直线MN为y轴建立坐标系.我们把横纵坐标都是整数的点叫做整数点,请写出⊙C上位于第二象限和第三象限的整数点的坐标
如图,AB是⊙C的弦,直径MN⊥AB于点O,MN=10,AB=8,以直线AB为x轴,直线MN为y轴建立坐标系.我们把横纵坐标都是整数的点叫做整数点,请写出⊙C上位于第二象限和第三象限的整数点的坐标已知(a+b)2=11,(a-b)2=7,则a2+b2等于( )
| A、4 | B、18 | C、9 | D、8 |
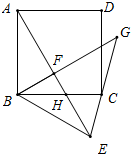 已知:正方形ABCD中,点F为正方形内一点(AF>BF),AF⊥BF,把△AFB沿BF所在的直线翻折,使点A落在点E处,AE交BC于点H,连接CE.
已知:正方形ABCD中,点F为正方形内一点(AF>BF),AF⊥BF,把△AFB沿BF所在的直线翻折,使点A落在点E处,AE交BC于点H,连接CE. 如图,已知DE∥BC,AD=5,DB=3,则S△ADE:S四边形DBCE=
如图,已知DE∥BC,AD=5,DB=3,则S△ADE:S四边形DBCE=