题目内容
6.计算:(-1)5-($\sqrt{5}$-1)0+$\root{3}{-27}$=-5.分析 首先分别求出(-1)5、($\sqrt{5}$-1)0、$\root{3}{-27}$的值各是多少;然后根据实数的运算顺序,从左向右依次计算,求出算式(-1)5-($\sqrt{5}$-1)0+$\root{3}{-27}$的值是多少即可.
解答 解:(-1)5-($\sqrt{5}$-1)0+$\root{3}{-27}$
=-1-1-3
=-2-3
=-5
故答案为:-5.
点评 (1)此题主要考查了实数的运算,要熟练掌握,解答此题的关键是要明确:在进行实数运算时,和有理数运算一样,要从高级到低级,即先算乘方、开方,再算乘除,最后算加减,有括号的要先算括号里面的,同级运算要按照从左到有的顺序进行.另外,有理数的运算律在实数范围内仍然适用.
(2)此题还考查了零指数幂的运算,要熟练掌握,解答此题的关键是要明确:①a0=1(a≠0);②00≠1.
(3)此题还考查了立方根的性质和应用,要熟练掌握,解答此题的关键是要明确:一个数的立方根只有一个,正数的立方根是正数,负数的立方根是负数,0的立方根是0.

练习册系列答案
相关题目
14.如图,Rt△ABC以1m/s的速度沿直线l匀速向矩形FCDE移动,直到点B与点D重合,AB=FC,设x秒时,三角形与矩形重叠部分的面积为ycm2,y与x的函数图象如图,则下列说法中错误的是( )
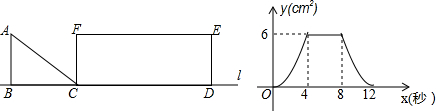

| A. | BC=4 | |
| B. | AB=3 | |
| C. | CD=10 | |
| D. | 当0≤x≤4时,y与x的函数关系式为y=$\frac{3}{8}$x2 |
1.已知反比例函数y=-$\frac{3}{x}$,下列结论不正确的是( )
| A. | 图象必经过点(-1,3) | B. | 若x>1,则-3<y<0 | ||
| C. | 图象在第二、四象限内 | D. | y随x的增大而增大 |
11.若关于x一元二次方程x2-10x+k+1=0有两个相等的实数根,则k的值为( )
| A. | 8 | B. | 9 | C. | 12 | D. | 24 |
16.已知一次函数y=kx+2经过点(1,0),则k的值是( )
| A. | -$\frac{1}{2}$ | B. | $\frac{1}{2}$ | C. | -2 | D. | 2 |
 在?ABCD中,过点D作DE⊥AB于点E,点F 在边CD上,DF=BE,连接AF,BF.
在?ABCD中,过点D作DE⊥AB于点E,点F 在边CD上,DF=BE,连接AF,BF.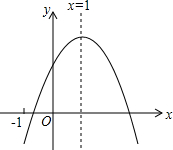 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列5个结论:①abc>0;②a+b+c>0;③4a+2b+c<0;④b<a+c;⑤b2-4ac>0,其中正确的结论有②⑤.(只填序号)
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列5个结论:①abc>0;②a+b+c>0;③4a+2b+c<0;④b<a+c;⑤b2-4ac>0,其中正确的结论有②⑤.(只填序号)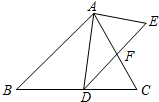 如图,在△ABC中,点D是BC上的点,∠DAC=∠ADE,AC交DF于点F,且AC=DE.
如图,在△ABC中,点D是BC上的点,∠DAC=∠ADE,AC交DF于点F,且AC=DE.