题目内容
5.下列各式计算正确的是( )| A. | $\sqrt{\frac{-4}{-9}}$=$\frac{\sqrt{-4}}{\sqrt{-9}}$=$\frac{-2}{-3}$=$\frac{2}{3}$ | B. | $\sqrt{4\frac{2}{9}}$=$\sqrt{\frac{38}{9}}$=2$\frac{1}{3}$$\sqrt{2}$ | ||
| C. | $\sqrt{\frac{3}{7}}$÷$\sqrt{3\frac{1}{2}}$=$\frac{\sqrt{6}}{7}$ | D. | $\sqrt{\frac{8}{25}}$=5$\sqrt{8}$ |
分析 A:计算商的算术平方根时,在使用性质a•b=a•b(a≥0,b≥0)时,一定要注意a≥0,b≥0的条件限制,据此判断即可.
B:应用商的算术平方根的性质判断即可.
C:根据二次根式的除法的运算方法判断即可.
D:应用商的算术平方根的性质判断即可.
解答 解:∵$\sqrt{\frac{-4}{-9}}=\frac{\sqrt{4}}{\sqrt{9}}=\frac{2}{3}$,
∴选项A不正确;
∵$\sqrt{4\frac{2}{9}}=\sqrt{\frac{38}{9}}=\frac{\sqrt{38}}{3}$,
∴选项B不正确;
∵$\sqrt{\frac{3}{7}}÷\sqrt{3\frac{1}{2}}=\frac{\sqrt{6}}{7}$,
∴选项C正确;
∵$\sqrt{\frac{8}{25}}=\frac{\sqrt{8}}{\sqrt{25}}=\frac{2\sqrt{2}}{5}$,
∴选项D不正确.
故选:C.
点评 此题主要考查了二次根式的乘除法,要熟练掌握,解答此题的关键是要明确:在使用性质a•b=a•b(a≥0,b≥0)时,一定要注意a≥0,b≥0的条件限制,如果a<0,b<0,使用该性质会使二次根式无意义;同样的在使用二次根式的乘法法则,商的算术平方根和二次根式的除法运算也是如此.

练习册系列答案
相关题目
14.如图,Rt△ABC以1m/s的速度沿直线l匀速向矩形FCDE移动,直到点B与点D重合,AB=FC,设x秒时,三角形与矩形重叠部分的面积为ycm2,y与x的函数图象如图,则下列说法中错误的是( )
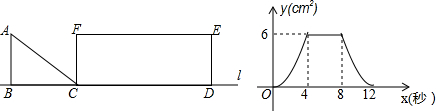

| A. | BC=4 | |
| B. | AB=3 | |
| C. | CD=10 | |
| D. | 当0≤x≤4时,y与x的函数关系式为y=$\frac{3}{8}$x2 |
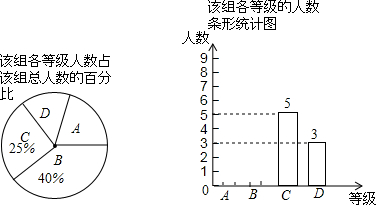
 在?ABCD中,过点D作DE⊥AB于点E,点F 在边CD上,DF=BE,连接AF,BF.
在?ABCD中,过点D作DE⊥AB于点E,点F 在边CD上,DF=BE,连接AF,BF.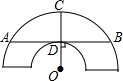 如图是一个古代车轮的碎片,小明为求其外圆半径,连接外圆上的两点A、B,并使AB与车轮内圆相切于点D,半径为OC⊥AB交外圆于点C.测得CD=10cm,AB=60cm,则这个车轮的外圆半径是50cm.
如图是一个古代车轮的碎片,小明为求其外圆半径,连接外圆上的两点A、B,并使AB与车轮内圆相切于点D,半径为OC⊥AB交外圆于点C.测得CD=10cm,AB=60cm,则这个车轮的外圆半径是50cm. 如图,△ABC中,∠ABC=68°,将△ABC绕点B逆时针旋转到△A′BC′的位置,使得AA′∥BC,则∠CBC′=48°.
如图,△ABC中,∠ABC=68°,将△ABC绕点B逆时针旋转到△A′BC′的位置,使得AA′∥BC,则∠CBC′=48°.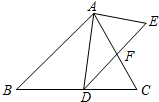 如图,在△ABC中,点D是BC上的点,∠DAC=∠ADE,AC交DF于点F,且AC=DE.
如图,在△ABC中,点D是BC上的点,∠DAC=∠ADE,AC交DF于点F,且AC=DE.