题目内容
9.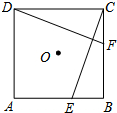 如图,E、F分别是正方形ABCD的边AB、BC上的点,BE=CF,连接CE、DF.△CDF可以看作是将△BCE绕正方形ABCD的中心O按逆时针方向旋转得到.则旋转的角度为90°.
如图,E、F分别是正方形ABCD的边AB、BC上的点,BE=CF,连接CE、DF.△CDF可以看作是将△BCE绕正方形ABCD的中心O按逆时针方向旋转得到.则旋转的角度为90°.
分析 根据旋转性质得出旋转后C到D,只要根据正方形的性质和三角形的内角和定理求出∠COD即可.
解答 解:将△CBE绕正方形的对角线交点O按顺时针方向旋转到△CDF时,C和D重合,
即∠COD是旋转角,
∵四边形ABCD是正方形,
∴∠OCD=∠ODC=45°,
∴∠COD=180°-45°-45°=90°,
即旋转角是90°,
故答案为90.
点评 本题主要考查了旋转的性质,以及正多边形的性质,正确理解正多边形的性质以及旋转角(对应点与旋转中心所连线段的夹角等于旋转角)是解题的关键.

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案
相关题目
4.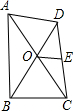 如图,在四边形ABCD中,∠ABC=90°,对角线AC、BD交于点O,AO=CO,∠AOD=∠ADO,E是DC边的中点,下列结论中,错误的是( )
如图,在四边形ABCD中,∠ABC=90°,对角线AC、BD交于点O,AO=CO,∠AOD=∠ADO,E是DC边的中点,下列结论中,错误的是( )
 如图,在四边形ABCD中,∠ABC=90°,对角线AC、BD交于点O,AO=CO,∠AOD=∠ADO,E是DC边的中点,下列结论中,错误的是( )
如图,在四边形ABCD中,∠ABC=90°,对角线AC、BD交于点O,AO=CO,∠AOD=∠ADO,E是DC边的中点,下列结论中,错误的是( )| A. | OE=$\frac{1}{2}$AD | B. | OE=$\frac{1}{2}$OB | C. | OE=$\frac{1}{2}$OC | D. | OE=$\frac{1}{2}$BC |
14.如图,Rt△ABC以1m/s的速度沿直线l匀速向矩形FCDE移动,直到点B与点D重合,AB=FC,设x秒时,三角形与矩形重叠部分的面积为ycm2,y与x的函数图象如图,则下列说法中错误的是( )
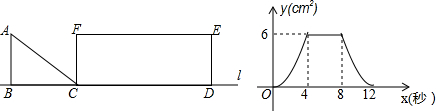

| A. | BC=4 | |
| B. | AB=3 | |
| C. | CD=10 | |
| D. | 当0≤x≤4时,y与x的函数关系式为y=$\frac{3}{8}$x2 |
1.已知反比例函数y=-$\frac{3}{x}$,下列结论不正确的是( )
| A. | 图象必经过点(-1,3) | B. | 若x>1,则-3<y<0 | ||
| C. | 图象在第二、四象限内 | D. | y随x的增大而增大 |
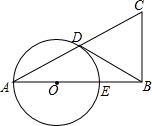 已知在△ABC中,∠B=90°,以AB上的一点O为圆心,以OA为半径的圆交AC于点D,交AB于点E.
已知在△ABC中,∠B=90°,以AB上的一点O为圆心,以OA为半径的圆交AC于点D,交AB于点E.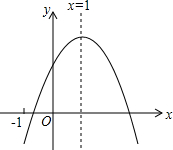 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列5个结论:①abc>0;②a+b+c>0;③4a+2b+c<0;④b<a+c;⑤b2-4ac>0,其中正确的结论有②⑤.(只填序号)
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列5个结论:①abc>0;②a+b+c>0;③4a+2b+c<0;④b<a+c;⑤b2-4ac>0,其中正确的结论有②⑤.(只填序号)