题目内容
4.甲、乙、丙、丁四位同学分别站在正方形场地的四个顶点A、B、C、D处,每个人都以相同的速度沿着正方形的边同时出发随机走向相邻的顶点处,那么甲、乙、丙、丁四位同学互不相遇的概率是$\frac{1}{8}$.分析 找出随机走的所有情况,以及相遇的情况数,即可求出所求的概率.
解答 解:∵甲、乙、丙、丁四位同学分别站在正方形场地的四个顶点A、B、C、D处,每个人都以相同的速度沿着正方形的边同时出发随机走向相邻的顶点处,共有2×2×2×2×2=16(种)等可能的结果,其中甲、乙、丙、丁四位同学互不相遇的有2种情况,
∴甲、乙、丙、丁四位同学互不相遇的概率是:$\frac{2}{16}$=$\frac{1}{8}$.
故答案为:$\frac{1}{8}$.
点评 此题考查了列表法与树状图法,用到的知识点为:概率=所求情况数与总情况数之比.

练习册系列答案
相关题目
14.如图,Rt△ABC以1m/s的速度沿直线l匀速向矩形FCDE移动,直到点B与点D重合,AB=FC,设x秒时,三角形与矩形重叠部分的面积为ycm2,y与x的函数图象如图,则下列说法中错误的是( )
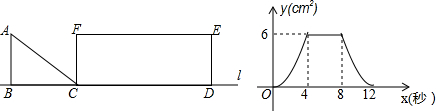

| A. | BC=4 | |
| B. | AB=3 | |
| C. | CD=10 | |
| D. | 当0≤x≤4时,y与x的函数关系式为y=$\frac{3}{8}$x2 |
16.已知一次函数y=kx+2经过点(1,0),则k的值是( )
| A. | -$\frac{1}{2}$ | B. | $\frac{1}{2}$ | C. | -2 | D. | 2 |
14.已知二次函数y=x2+2x-k,小聪利用计算器列出了下表:
那么方程x2+2x-k=0的一个近似根是( )
| x | -4.1 | -4.2 | -4.3 | -4.4 |
| x2+2x-k | -1.39 | -0.76 | -0.11 | 0.56 |
| A. | -4.1 | B. | -4.2 | C. | -4.3 | D. | -4.4 |
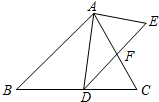 如图,在△ABC中,点D是BC上的点,∠DAC=∠ADE,AC交DF于点F,且AC=DE.
如图,在△ABC中,点D是BC上的点,∠DAC=∠ADE,AC交DF于点F,且AC=DE. 如图,AB为⊙O的直径,PD切⊙O于点C,交AB的延长线于点D,且∠D=2∠CAD.若CD=2,则BD的长为2$\sqrt{2}$-2.
如图,AB为⊙O的直径,PD切⊙O于点C,交AB的延长线于点D,且∠D=2∠CAD.若CD=2,则BD的长为2$\sqrt{2}$-2.