题目内容
3.如图,△ABC中,∠ACB=90?,AB=10,tanA=$\frac{1}{2}$.点P是斜边AB上一个动点.过点P作PQ⊥AB,垂足为P,交边AC(或边CB)于点Q,设AP=x,△APQ的面积为y,则y与x之间的函数图象大致为( )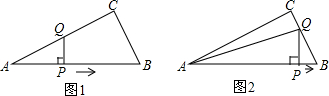
| A. | 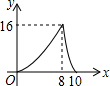 | B. | 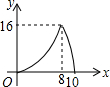 | C. | 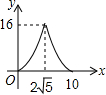 | D. | 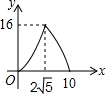 |
分析 分点Q在AC上和BC上两种情况进行讨论即可.
解答 解:当点Q在AC上时,
∵tanA=$\frac{1}{2}$,AP=x,
∴PQ=$\frac{1}{2}$x,
∴y=$\frac{1}{2}$×AP×PQ=$\frac{1}{2}$×x×$\frac{1}{2}$x=$\frac{1}{4}$x2;
当点Q在BC上时,如下图所示: ∵AP=x,AB=10,tanA=$\frac{1}{2}$,
∵AP=x,AB=10,tanA=$\frac{1}{2}$,
∴BP=10-x,PQ=2BP=20-2x,
∴y=$\frac{1}{2}$•AP•PQ=$\frac{1}{2}$×x×(20-2x)=-x2+10x,
∴该函数图象前半部分是抛物线开口向上,后半部分也为抛物线开口向下.并且当Q点在C时,x=8,y=16.
故选:B.
点评 本题考查动点问题的函数图象,有一定难度,解题关键是注意点Q在BC上这种情况.

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
14.如图,Rt△ABC以1m/s的速度沿直线l匀速向矩形FCDE移动,直到点B与点D重合,AB=FC,设x秒时,三角形与矩形重叠部分的面积为ycm2,y与x的函数图象如图,则下列说法中错误的是( )
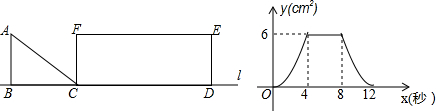

| A. | BC=4 | |
| B. | AB=3 | |
| C. | CD=10 | |
| D. | 当0≤x≤4时,y与x的函数关系式为y=$\frac{3}{8}$x2 |
11.若关于x一元二次方程x2-10x+k+1=0有两个相等的实数根,则k的值为( )
| A. | 8 | B. | 9 | C. | 12 | D. | 24 |
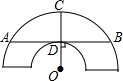 如图是一个古代车轮的碎片,小明为求其外圆半径,连接外圆上的两点A、B,并使AB与车轮内圆相切于点D,半径为OC⊥AB交外圆于点C.测得CD=10cm,AB=60cm,则这个车轮的外圆半径是50cm.
如图是一个古代车轮的碎片,小明为求其外圆半径,连接外圆上的两点A、B,并使AB与车轮内圆相切于点D,半径为OC⊥AB交外圆于点C.测得CD=10cm,AB=60cm,则这个车轮的外圆半径是50cm.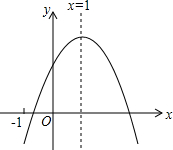 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列5个结论:①abc>0;②a+b+c>0;③4a+2b+c<0;④b<a+c;⑤b2-4ac>0,其中正确的结论有②⑤.(只填序号)
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列5个结论:①abc>0;②a+b+c>0;③4a+2b+c<0;④b<a+c;⑤b2-4ac>0,其中正确的结论有②⑤.(只填序号) 如图是正方体的一种展开图,其中每个面上都有一个数字,那么在原正方体中,与数字6相对面上的数字是( )
如图是正方体的一种展开图,其中每个面上都有一个数字,那么在原正方体中,与数字6相对面上的数字是( )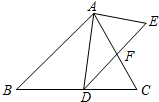 如图,在△ABC中,点D是BC上的点,∠DAC=∠ADE,AC交DF于点F,且AC=DE.
如图,在△ABC中,点D是BC上的点,∠DAC=∠ADE,AC交DF于点F,且AC=DE.