题目内容
5.先化简、再求值(1)(x+2)2+(x+1)(x-5),其中x=$\frac{7}{8}$
(2)[(xy+2)(xy-2)-2(x2y2-2)]÷(xy),其中x=10,y=-$\frac{1}{25}$.
分析 (1)根据完全平方式和多项式乘多项式即可化简题目中的式子,然后将x的值代入即可解答本题;
(2)根据平方差公式和单项式乘多项式、整式的除法即可化简题目中的式子,然后将x的值代入即可解答本题.
解答 解:(1)(x+2)2+(x+1)(x-5)
=x2+4x+4+x2-4x-5
=2x2-1,
当x=$\frac{7}{8}$时,原式=$2×(\frac{7}{8})^{2}-1$=$\frac{17}{32}$;
(2)[(xy+2)(xy-2)-2(x2y2-2)]÷(xy)
=[x2y2-4-2x2y2+4]÷(xy)
=(-x2y2)÷(xy)
=-xy,
当x=10,y=-$\frac{1}{25}$时,原式=$-10×(-\frac{1}{25})$=$\frac{2}{5}$.
点评 本题考查整式的混合运算-化简求值,解题的关键是明确整式的混合运算的计算方法.

练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案
相关题目
15.下列解方程的各种变形中,正确的是( )
| A. | 由5x=4x+1可得4x-5x=1 | B. | 由3(x-1)-2(2x-3)=1可得3x-3-4x-6=1 | ||
| C. | 由$\frac{x+2}{4}$-1=$\frac{2x-3}{6}$可得3(x+2)-1=2(2x-3) | D. | 由$\frac{1}{2}$x=$\frac{1}{4}$可得x=$\frac{1}{2}$ |
10.下列各式错误的是( )
| A. | -4>-5 | B. | -(-3)=3 | C. | -|-4|=4 | D. | 16÷(-4)2=1 |
17.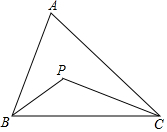 如图,在△ABC中,∠BAC=56°,∠ABC=74°,BP、CP分别平分∠ABC和∠ACB,则∠BPC=( )
如图,在△ABC中,∠BAC=56°,∠ABC=74°,BP、CP分别平分∠ABC和∠ACB,则∠BPC=( )
 如图,在△ABC中,∠BAC=56°,∠ABC=74°,BP、CP分别平分∠ABC和∠ACB,则∠BPC=( )
如图,在△ABC中,∠BAC=56°,∠ABC=74°,BP、CP分别平分∠ABC和∠ACB,则∠BPC=( )| A. | 102° | B. | 112° | C. | 115° | D. | 118° |
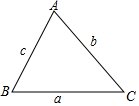 如图,在锐角三角形中,
如图,在锐角三角形中,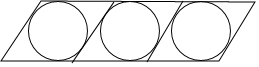 如图,花边带上菱形的内切圆半径均为1cm,若菱形有一个内角为60°,且这条花边带有50个圆和50个菱形,求这条花边上、下边长的和.
如图,花边带上菱形的内切圆半径均为1cm,若菱形有一个内角为60°,且这条花边带有50个圆和50个菱形,求这条花边上、下边长的和.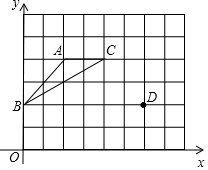 如图,在坐标系的第一象限建立网格,网格中的每个小正方形边长都为1,格点△ABC的顶点坐标分别为A(2,4)、B(0,2)、C(4,4).
如图,在坐标系的第一象限建立网格,网格中的每个小正方形边长都为1,格点△ABC的顶点坐标分别为A(2,4)、B(0,2)、C(4,4).